题目内容
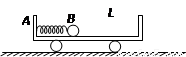
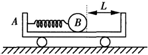 如图所示,一辆质量M=3kg的小车A静止在光滑的水平面上,小车上有一质量m=1kg的光滑小球B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小球与小车右壁距离为L,解除锁定,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,求:
如图所示,一辆质量M=3kg的小车A静止在光滑的水平面上,小车上有一质量m=1kg的光滑小球B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小球与小车右壁距离为L,解除锁定,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,求:(1)小球脱离弹簧时小球和小车各自的速度大小.
(2)在整个过程中,小车移动的距离.
分析:解除锁定后弹簧的弹性势能转化为系统动能,根据动量守恒和能量守恒列出等式求解
解答:解:(1)除锁定后弹簧的弹性势能转化为系统动能,根据动量守恒和能量守恒列出等式得
mv1-Mv2=0
m
+
M
=Ep
解得:v1=3m/s v2=1m/s
(2)根据动量守恒和各自位移关系得
=M
x1+x2=L
解得:x2=
答:(1)小球脱离弹簧时小球和小车各自的速度大小是v1=3m/s v2=1m/s.
(2)在整个过程中,小车移动的距离是
.
mv1-Mv2=0
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
解得:v1=3m/s v2=1m/s
(2)根据动量守恒和各自位移关系得
| x1 |
| t |
| x2 |
| t |
x1+x2=L
解得:x2=
| L |
| 4 |
答:(1)小球脱离弹簧时小球和小车各自的速度大小是v1=3m/s v2=1m/s.
(2)在整个过程中,小车移动的距离是
| L |
| 4 |
点评:本题是动量守恒和能量守恒的综合应用.解除弹簧的锁定后,系统所受合力为零,遵守动量守恒和能量守恒.

练习册系列答案
相关题目
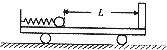 (2013?宝鸡三模)如图所示,一辆质量M=3kg的小车静止在光滑的水平面上,小车上固定一装有弹簧的弹射装置,用一质量m=2kg的小球将弹簧压缩并锁定,此时弹簧的弹性势能为Ep=15J,小球与车右壁的距离为L=0.5m.解除锁定,小球被弹簧弹开后与小车右臂粘层碰撞并粘住,求:
(2013?宝鸡三模)如图所示,一辆质量M=3kg的小车静止在光滑的水平面上,小车上固定一装有弹簧的弹射装置,用一质量m=2kg的小球将弹簧压缩并锁定,此时弹簧的弹性势能为Ep=15J,小球与车右壁的距离为L=0.5m.解除锁定,小球被弹簧弹开后与小车右臂粘层碰撞并粘住,求: 如图所示,一辆质量m=2.0t的小轿车,驶过半径R=90m的一段圆弧形桥面,重力加速度g=10m/s2.求:
如图所示,一辆质量m=2.0t的小轿车,驶过半径R=90m的一段圆弧形桥面,重力加速度g=10m/s2.求: