题目内容
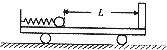 (2013?宝鸡三模)如图所示,一辆质量M=3kg的小车静止在光滑的水平面上,小车上固定一装有弹簧的弹射装置,用一质量m=2kg的小球将弹簧压缩并锁定,此时弹簧的弹性势能为Ep=15J,小球与车右壁的距离为L=0.5m.解除锁定,小球被弹簧弹开后与小车右臂粘层碰撞并粘住,求:
(2013?宝鸡三模)如图所示,一辆质量M=3kg的小车静止在光滑的水平面上,小车上固定一装有弹簧的弹射装置,用一质量m=2kg的小球将弹簧压缩并锁定,此时弹簧的弹性势能为Ep=15J,小球与车右壁的距离为L=0.5m.解除锁定,小球被弹簧弹开后与小车右臂粘层碰撞并粘住,求:①小球脱离弹射装置时小球和小车各自的速度大小:
②在整个过程中,小车移动的距离.
分析:(1)根据动量守恒定律和能量守恒定律求出小球脱离弹射装置时小球和小车各自的速度大小.
(2)根据动量守恒定律,结合小球和小车的位移之和等于L,求出在整个过程中,小车移动的距离.
(2)根据动量守恒定律,结合小球和小车的位移之和等于L,求出在整个过程中,小车移动的距离.
解答:解:(1)设小球脱离弹簧时小球和小车各自的速度大小分别为v1和v2,由动量守恒定律得:
mv1-Mv2=0
Ep=
mv12+
Mv22
联立两式解得:v1=3m/s,v2=2m/s.
(2)设整个运动过程中所用的时间为t,小球移动距离为x1,小车移动距离为x2,可得:
m
=M
x1+x2=L
解得:x2=
L=0.2m.
答:(1)小球脱离弹射装置时小球和小车各自的速度大小为3m/s、2m/s.
(2)在整个过程中,小车移动的距离0.2m.
mv1-Mv2=0
Ep=
| 1 |
| 2 |
| 1 |
| 2 |
联立两式解得:v1=3m/s,v2=2m/s.
(2)设整个运动过程中所用的时间为t,小球移动距离为x1,小车移动距离为x2,可得:
m
| x1 |
| t |
| x2 |
| t |
x1+x2=L
解得:x2=
| 2 |
| 5 |
答:(1)小球脱离弹射装置时小球和小车各自的速度大小为3m/s、2m/s.
(2)在整个过程中,小车移动的距离0.2m.
点评:解决本题的关键知道小球和小车组成的系统,动量守恒,结合动量守恒定律和能量守恒定律进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?宝鸡三模)粗细均匀的U形管竖直放置,右端封闭,左管内有一个重力和摩擦都不计的活塞,管内水银把气体分隔成A、B两部分.当大气压强为P0=75cmHg、温度为t0=27℃时,管内水银面在同一高度,两部分气体的长度均为L0=20cm.
(2013?宝鸡三模)粗细均匀的U形管竖直放置,右端封闭,左管内有一个重力和摩擦都不计的活塞,管内水银把气体分隔成A、B两部分.当大气压强为P0=75cmHg、温度为t0=27℃时,管内水银面在同一高度,两部分气体的长度均为L0=20cm. (2013?宝鸡三模)(此题属多选)如图所示是某电场中的一条电场线,M、N是该电场线上的两点,则以下判断中正确的是( )
(2013?宝鸡三模)(此题属多选)如图所示是某电场中的一条电场线,M、N是该电场线上的两点,则以下判断中正确的是( ) (2013?宝鸡三模)(此题属多选)如图所示,质量为m的物体与转台之问的动摩擦因数为μ,物体与转轴间距离为R,物体随转台由静止开始转动,当转台转速增加到某一值后转台开始匀速转动,整个过程中物体相对于转台静止不动,则以下判断正确的是( )
(2013?宝鸡三模)(此题属多选)如图所示,质量为m的物体与转台之问的动摩擦因数为μ,物体与转轴间距离为R,物体随转台由静止开始转动,当转台转速增加到某一值后转台开始匀速转动,整个过程中物体相对于转台静止不动,则以下判断正确的是( ) (2013?宝鸡三模)如图所示,人用轻绳通过定滑轮吊起重物A.当人匀速向右运动的过程中,下列说法正确的是( )
(2013?宝鸡三模)如图所示,人用轻绳通过定滑轮吊起重物A.当人匀速向右运动的过程中,下列说法正确的是( )