题目内容
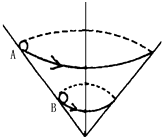
【题目】如图所示,倾角为![]() 的部分粗糙的斜面轨道和两个光滑半圆轨道组成翘尾巴的S形轨道.两个光滑半圆轨道半径都为R=0.2 m,其连接处CD之间留有很小空隙,刚好能够使小球通过,CD之间距离可忽略.斜面上端有一弹簧,弹簧上端固定在斜面上的挡板上,弹黄下端与一个可视为质点、质量为m=0.02 kg的小球接触但不固定,此时弹簧处于压缩状态并锁定,弹簧的弹性势能Ep=0.27 J.现解除弹簧的锁定,小球从A点出发,经翘尾巴的S形轨道运动后从E点水平飞出,落到水平地面上,落点到与E点在同一竖直线上B点的距离为s=2.0 m;己知斜面轨道的A点与水平面上B点之间的高度为h=l.0 m,小球与斜面的粗糙部分间的动摩擦因数为0.75;小球从斜面到达半圆轨道通过B点时,前后速度大小不变,不计空气阻力,(sin 370=0.6,cos 370=0.8.取g=10 m/s2).求:
的部分粗糙的斜面轨道和两个光滑半圆轨道组成翘尾巴的S形轨道.两个光滑半圆轨道半径都为R=0.2 m,其连接处CD之间留有很小空隙,刚好能够使小球通过,CD之间距离可忽略.斜面上端有一弹簧,弹簧上端固定在斜面上的挡板上,弹黄下端与一个可视为质点、质量为m=0.02 kg的小球接触但不固定,此时弹簧处于压缩状态并锁定,弹簧的弹性势能Ep=0.27 J.现解除弹簧的锁定,小球从A点出发,经翘尾巴的S形轨道运动后从E点水平飞出,落到水平地面上,落点到与E点在同一竖直线上B点的距离为s=2.0 m;己知斜面轨道的A点与水平面上B点之间的高度为h=l.0 m,小球与斜面的粗糙部分间的动摩擦因数为0.75;小球从斜面到达半圆轨道通过B点时,前后速度大小不变,不计空气阻力,(sin 370=0.6,cos 370=0.8.取g=10 m/s2).求:
(1)小球从E点水平飞出时的速度大小;
(2)小球对B点轨道的压力;
(3)斜面粗糙部分的长度x.

【答案】(1)5m/s(2)4.3N,方向竖直向下(3)0.5m
【解析】(1)小球从E点水平飞出做平抛运动,设小球从E点水平飞出时的速度大小为vE,由平抛运动规律知,
s=vEt,
4R=![]() gt2,
gt2,
联立解得vE=![]() =5 m/s
=5 m/s
(2)小球从B点运动到E点的过程,由机械能守恒有
![]() mv B2=mg×4R+
mv B2=mg×4R+![]() mv E2
mv E2
解得vB2=8gR+![]() ,
,
则vB=![]() m/s
m/s
在B点有FN-mg=m![]()
所以FN=9mg+![]() =4.3 N
=4.3 N
由牛顿第三定律可知F′N=FN=4.3 N,方向竖直向下
(3)小球沿斜面下滑到B点的过程,由功能关系有:mgh-μmgcos 37°x=![]() mvB2-Ep
mvB2-Ep
解得x=0.5 m.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目