题目内容
20. 探究单摆的运动,用单摆测定重力加速度
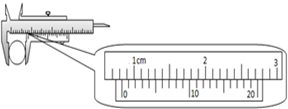
探究单摆的运动,用单摆测定重力加速度(1)某同学通过游标卡尺测定某小球的直径,测量的结果如图所示,则该小球的直径为0.830cm
(2)利用单摆测重力加速度的实验中,如果偏角小于5°,但测出的重力加速度的数值偏大,可能的原因是D
A.振幅较小
B.测摆长时,只量出摆线的长度,没有从悬挂点量到摆球中心
C.数振动次数时,少计了一次
D.数振动次数时,多计了一次
(3)某同学用单摆测重力加速度,他将单摆挂起后,进行了如下实验步骤:
①测摆长L:用米尺量出摆线的长度;
②测周期T:将摆球拉起,摆角小于5°时自由释放摆球,在摆球某次通过最低点时按下秒表开始计时,将此作为第一次,接着一直数到摆球第60次通过最低点时,按下秒表停止计时,读出这段时间t,算出单摆的周期T=$\frac{t}{60}$;
③将所测量的 L和T值代入单摆周期公式,算出重力加速度g,将它作为实验的最后结果写进实验报告中去.
请在下面的空白处,分别指出各步骤中遗漏或错误的地方.
①要用卡尺测出摆球的直径d,摆长l等于摆线长加上$\frac{d}{2}$;
②单摆周期T=$\frac{t}{29.5}$;
③改变摆长,多次测量,取g的平均值作为实验的最后结果.
分析 (1)游标卡尺主尺与游标尺示数之和是游标卡尺的示数.
(2)根据单摆周期公式求出重力加速度的表达式,然后分析实验误差.
(3)在用单摆测重力加速度的实验中,摆长等于摆线的长度加上摆球的半径,周期等于完成一次全振动的时间,用时间除以全振动的次数.利用多次测量取平均值求出当地的重力加速度.
解答 解:(1)由图示游标卡尺可知,其示数为:8mm+6×0.05mm=8.30mm=0.830cm;
(2)由单摆周期公式:T=2π$\sqrt{\frac{L}{g}}$可知,重力加速度:g=$\frac{4{π}^{2}L}{{T}^{2}}$;
A、单摆的周期与振幅无关,振幅较小不影响重力加速度的测量值,故A错误;
B、测摆长时,只量出摆线的长度,没有从悬挂点量到摆球中心,所测摆长L偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测重力加速度g偏小,故B正确;
C、数振动次数时,少计了一次,所测周期T偏大,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测g偏小,故C错误;
D、数振动次数时,多计了一次,所测周期T偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知,所测g偏大,故D正确;故选D;
(3)摆长等于摆线长度与摆球半径之和,因此实验 步骤①错误.
单摆完成一次全振动需要的时间是一个周期,一次全振动两次经过最低点.在摆球某次通过最低点时按下秒表开始计时,将此作为第一次,接着一直数到摆球第60次通过最低点时,按下秒表停止计时,读出这段时间t,算出单摆的周期T=$\frac{t}{29.5}$,故实验步骤②错误.
为减小实验误差应进行多次测量求平均值,实验步骤③存在疏漏;
故答案为:(1)0.830;(2)D;(3)①要用卡尺测出摆球的直径d,摆长l等于摆线长加上$\frac{d}{2}$;②单摆周期T=$\frac{t}{29.5}$;③改变摆长,多次测量,取g的平均值作为实验的最后结果.
点评 本题考查了游标卡尺读数、实验误差分析、实验步骤操作分析,知道实验原理、掌握基础知识即可解题;游标卡尺主尺与游标尺示数之和是游标卡尺示数,游标卡尺不需要估读.

| A. | 瞬时速度是物体在某一位置或某一时刻的速度 | |
| B. | 平均速度等于某段时间内的位移与所用时间的比值 | |
| C. | 做变速运动的物体,平均速度是最大速度与最小速度的平均值 | |
| D. | 做变速运动的物体,平均速度是物体通过的路程与所用时间的比值 |
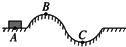 如图所示,一物体在凸凹不平的路面上行进,若物体与路面的动摩擦因数在各处均相同,为保持物体在A、B、C点匀速率行进,对物体的水平拉力F应该是( )
如图所示,一物体在凸凹不平的路面上行进,若物体与路面的动摩擦因数在各处均相同,为保持物体在A、B、C点匀速率行进,对物体的水平拉力F应该是( )| A. | 水平拉力F在A、B、C三点大小相等,方向相同 | |
| B. | 在A点的水平拉力F最小 | |
| C. | 在B点的水平拉力F最小 | |
| D. | 在C点的水平拉力F最大 |
| A. | 运动员在上升过程中对杆先做正功后做负功 | |
| B. | 撑杆恢复形变时,弹性势能完全转化为重力势能 | |
| C. | 运动员上升时阶段超重,下落阶段失重 | |
| D. | 运动员到达最高点时的速度一定为零 |
| A. | W1=W2=W3 P1=P2=P3 | B. | W1>W2>W3 P1>P2>P3 | ||
| C. | W1<W2<W3 P1<P2>P3 | D. | W1=W2=W3 P1=P2>P3 |
 如图所示,两个宽度相同但长度不同的台球框固定在水平面上,从两个框的长边上不同位置同时以相同的速度分别射出相同小球A和B,A距离左边框较远.设球与框边碰撞前后速度的大小不变,碰撞时间不计,方向与边框的夹角相同,忽略摩擦阻力.则两球第一次回到最初出发的长边的先后顺序是( )
如图所示,两个宽度相同但长度不同的台球框固定在水平面上,从两个框的长边上不同位置同时以相同的速度分别射出相同小球A和B,A距离左边框较远.设球与框边碰撞前后速度的大小不变,碰撞时间不计,方向与边框的夹角相同,忽略摩擦阻力.则两球第一次回到最初出发的长边的先后顺序是( )| A. | A球先回到出发长边 | |
| B. | B球先回到出发长边 | |
| C. | 两球同时回到出发长边 | |
| D. | 因两框长度不知,故无法确定哪一个球先回到出发框边 |
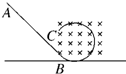 如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电,现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电,现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )| A. | 经过最高点时,三个小球的速度相等 | |
| B. | 经过最高点时,甲球的速度最小 | |
| C. | 运动过程中三个小球的机械能均不守恒 | |
| D. | 甲球的释放位置比乙球的高 |
