题目内容
11.盘在地面上的一根不均匀的金属链重30N,长1m,从甲端缓慢提至乙端恰好离地时需做功10J.如果改从乙端缓慢提至甲端恰好离地要做多少功?(取g=10m/s2)分析 缓慢将提起金属链,需要克服重力做功,根据重力做功公式W=Gh,h是重心上升的高度,求出金属链恰好离开地面时其重心离地面的高度,再确定将乙端从地面缓缓上提至甲端恰好离开地面重心上升的高度,即可求得需要做功多少.
解答 解:设金属链的重心离乙端距离为x,则将甲端从地面缓缓上提至乙端恰好离开地面时,有 W1=mgx=10 J,
可得:x=$\frac{{W}_{1}}{mg}$=$\frac{10}{30}$m=$\frac{1}{3}$m.
将乙端从地面缓缓上提至甲端恰好离开地面重心上升的高度为:
h2=L-h1=1m-$\frac{1}{3}$m=$\frac{2}{3}$m
需要做功为:W2=Gh2=30×$\frac{2}{3}$J=20J
答:改从乙端缓慢提至甲端恰好离地要做20J的功.
点评 解决本题时要注意:金属链不能看成质点,求重力做功时,要考虑重心上升的高度.

练习册系列答案
相关题目
7.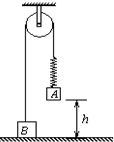 如图,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量分别为m、$\frac{3}{2}$m,开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度为v,此时物体B对地面恰好无压力,则下列说法中正确的是( )
如图,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量分别为m、$\frac{3}{2}$m,开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度为v,此时物体B对地面恰好无压力,则下列说法中正确的是( )
 如图,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量分别为m、$\frac{3}{2}$m,开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度为v,此时物体B对地面恰好无压力,则下列说法中正确的是( )
如图,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体A、B的质量分别为m、$\frac{3}{2}$m,开始时细绳伸直,用手托着物体A使弹簧处于原长且A与地面的距离为h,物体B静止在地面上.放手后物体A下落,与地面即将接触时速度为v,此时物体B对地面恰好无压力,则下列说法中正确的是( )| A. | 此时物体A的动能最大 | |
| B. | 此时物体B的加速度为零 | |
| C. | 下落过程A减少的重力势能等于A增加的动能 | |
| D. | 此时弹簧的弹性势能等于mgh-$\frac{1}{2}$mv2 |
8. 如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中 1、2、3、4、5…所示小球运动过程中每次曝光的位置.连 续两次曝光的时间间隔均为 T,每块砖的厚度为 d.根据图中的信息,下列判断正确的是( )
如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中 1、2、3、4、5…所示小球运动过程中每次曝光的位置.连 续两次曝光的时间间隔均为 T,每块砖的厚度为 d.根据图中的信息,下列判断正确的是( )
 如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中 1、2、3、4、5…所示小球运动过程中每次曝光的位置.连 续两次曝光的时间间隔均为 T,每块砖的厚度为 d.根据图中的信息,下列判断正确的是( )
如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中 1、2、3、4、5…所示小球运动过程中每次曝光的位置.连 续两次曝光的时间间隔均为 T,每块砖的厚度为 d.根据图中的信息,下列判断正确的是( )| A. | 能判定位置“1”是小球释放的初始位置 | |
| B. | 能求出小球下落的加速度为$\frac{2d}{T^2}$ | |
| C. | 能求出小球在位置“3”的速度为$\frac{7d}{2T}$ | |
| D. | 能判定小球下落过程中在做匀变速运动 |
16.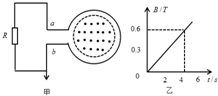 如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
 如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )| A. | 圆形线圈中产生的感应电动势E=6V | |
| B. | 电阻R两端的电压为4.5V | |
| C. | 通过电阻R的电流为I=1.5A | |
| D. | 在0-4s时间内,b端的电势比a端的电势低 |
3. 如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,再由c点运动到b点最后离开弹簧,若不计弹簧质量和空气阻力,在小球由a→b→c→b的运动过程中,说法正确的是( )
如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,再由c点运动到b点最后离开弹簧,若不计弹簧质量和空气阻力,在小球由a→b→c→b的运动过程中,说法正确的是( )
 如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,再由c点运动到b点最后离开弹簧,若不计弹簧质量和空气阻力,在小球由a→b→c→b的运动过程中,说法正确的是( )
如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,再由c点运动到b点最后离开弹簧,若不计弹簧质量和空气阻力,在小球由a→b→c→b的运动过程中,说法正确的是( )| A. | 小球的机械能守恒 | |
| B. | 小球在b点时动能最大 | |
| C. | 小球在运动过程中存在动能减少而机械能增大的过程 | |
| D. | 小球从b点运动到c点的过程中,小球动能的减少量等于弹簧弹性势能的增加量 |
 面间的动摩擦因数μ=$\frac{1}{3}$,要使木箱能在水平路面上匀速移动,则绳上所加拉力F应为多大?
面间的动摩擦因数μ=$\frac{1}{3}$,要使木箱能在水平路面上匀速移动,则绳上所加拉力F应为多大? 探究单摆的运动,用单摆测定重力加速度
探究单摆的运动,用单摆测定重力加速度 光滑水平面上有三个木块A,B,C,其中木块A的质量mA=2m,木块B,C的质量均为m,开始时B,C均静止,木块A以初速度v0向右运动,与木块B发生弹性碰撞后分开,木块B又与木块C发生碰撞并粘在一起.求木块B的最终速度大小.
光滑水平面上有三个木块A,B,C,其中木块A的质量mA=2m,木块B,C的质量均为m,开始时B,C均静止,木块A以初速度v0向右运动,与木块B发生弹性碰撞后分开,木块B又与木块C发生碰撞并粘在一起.求木块B的最终速度大小.