题目内容
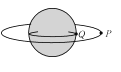
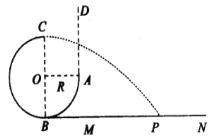
【题目】如图所示，半径为R的光滑圆弧轨道ABC固定在竖直平面内，O为圆心，OC竖直，OA水平，B为圆弧的最低点，B点紧靠一足够长的平台MN。D点位于A点正上方。现从D点无初速度释放一个可视为质点的小球，在A点进人圆弧轨道，从C点飞出后做平抛运动，不计空气阻力，重力加速度为g，求:
(1)通过计算说明小球能否重新落回到轨道内侧;
(2)若DA之间的高度差为3R，求小球落地点P到B点的距离L。
【答案】(1)小球不能重新落回到轨道内侧 (2)L=4R
【解析】
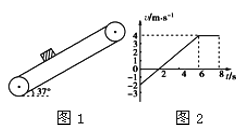
(1)设小球在C点的最小速度为v0，由牛顿第二定律
设小球下降高度R所用时间为t1。
在时间t1内的水平位移为
，解得
所以小球不能重新落回到轨道内侧。
(2)设小球到达C点的速度人小为vc，对小球从D点到C点的过程。
由动能定理
小球从C点飞出后做平抛运动，设经过时间以落到P点。竖直方向
水平方向
解得
L=4R
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】2019年12月7日至11日在日本东京举办了第十三届中日节能环保综合论坛，与会专家统计∶每使用1度（千瓦时）电，就相应消耗了0.4kg的标准煤，同时产生0.272kg碳粉尘，0.997kg二氧化碳，0.03kg二氧化硫，0.015kg氮氧化物。济宁市约有200万家庭，根据下表提供的数据，估算我市由于这4种用电器待机一昼夜产生的二氧化碳的质量约为（ ）
每户普通家庭用电平均数 | 1台平板电视机 | 1台空调 | 1台洗衣机 | 1台台式电脑 |
每台用电器平均待机功率（W） | 1 | 4 | 2 | 3 |
A.4.8×103kgB.4.8×104kgC.4.8×105kgD.4.8×106kg
