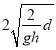��Ŀ����
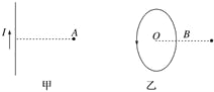
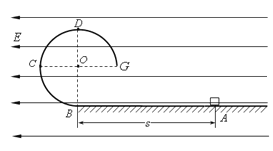
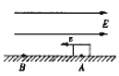
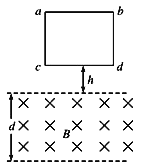
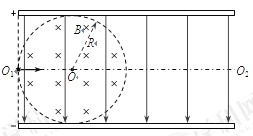
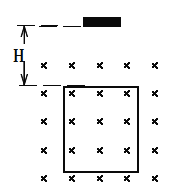
����Ŀ����һ�㹻���Ĺ⻬U�ε���̶�����ֱƽ���ڣ��ռ���ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȵĴ�СΪB��������ΪL��һ����Ϊ2m�Ľ��������ڵ���Ķ��ˣ���ʼ��������״̬����ͼ��ʾ��һ����Ϊm��С�������ɽ���������Ϸ�H�ߴ������ͷţ����������������������������������˺����һ�������˶���������һ��Ħ������������ĵ���R�����ಿ�ֵ�����ɺ�·���������ٶ�Ϊg��
�������������һ�θ߶Ⱥ�ʼ��vm���ٶ�������ֱ���˶�����vm�Ĵ�С
��������������˶������ٶ�����v1ʱ������Խ������ѹ�����
���𰸡���![]() ����
����![]() ��
��
��������
�ٵ����߿�ʼ��vm���ٶ������˶�ʱ������Ϊ�㣬��
3mg��F����0
�� F����BIL��![]() ����
����
![]()
������ã�
vm��![]()
�ڵ�������ͽ�������ٶȴﵽv1ʱ��������ٶ�Ϊa��
������壬����ţ�ٵڶ����ɵã�
3mg��![]() ��3ma
��3ma
�Խ��������������ţ�ٵڶ����ɵã�
mg��N��ma
������ý�����Խ������֧����Ϊ
N��![]()
��ţ�ٵ�������֪��������Խ������ѹ��Ϊ
N����N��![]()

��ϰ��ϵ�д�
�����Ŀ