题目内容
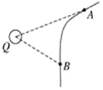
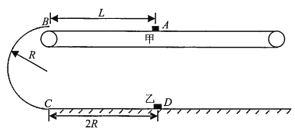
【题目】如图所示，半径为R、内壁光滑的半圆轨道固定于竖直平面内，下端C与水平地面相切，上端B与水平传送带的左端之间形成一小的狭缝，可让放在传送带上的小物块刚好通过，传送带以恒定速度
逆时针转动。水平地面D点放置一质量为3m的小物块乙，C、D间距为2R。现在传送带上的A处轻轻放上质量为m的小物块甲，A、B间的距离L=2R，它经传送带加速后，从B处沿半圆轨道滑下，再经C沿水平地面滑到D处，与物块乙相撞后立即粘在一起，继续向前滑行一段距离后静止。两物块均可视为质点，甲物块与传送带间的动摩擦因素及甲、乙两物块与地面间的动摩擦因素均为μ=0.5，重力加速度为g，传送带足够长：
(1)求甲物块经过半圆形轨道的C点时对轨道的压力FN；
(2)求两物块最终静止的位置离D点的距离x；
(3)若A、B间的距离L可调，求两物块最终静止的位置离D点的距离x随L变化的函数关系式。
【答案】(1)
，方向竖直向下；(2)
；(3)
【解析】
(1)根据动能定理物块从A至C有
对C点
解得支持力
，压力
，方向竖直向下
(2)甲物块由C至D
甲乙两物块碰撞
碰后一起运动至静止
最终静止的位置离D点的距离
(3)甲物块由A至D
甲乙两物块碰撞
碰后一起运动至静止
得
甲物块运动至B点恰好不脱轨 由
可得
物块运动至B点时恰好与传送带共速即
由速度位移公式
可得
综上所述：x随L变化的函数关系式为
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
