Question

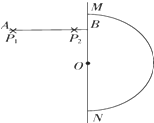
【题目】如图所示，质量M ＝0.8 kg的平板小车静止在光滑水平地面上，在小车左端放有质量m＝0.2 kg的物块A(可视为质点)，物块A与小车表面间的动摩擦因数μ＝0.2，在物块A正上方l＝0.45 m高处有一固定悬点，通过不可伸长的细绳悬挂一质量m0＝0.1 kg的物块B，把细绳拉至水平，由静止释放，物块B(视为质点)在最低点与物块A发生弹性碰撞。最终物块恰好不能从小车上滑下。重力加速度g＝10 m/s2。求：

(1)物块B与物块A碰撞后瞬间细绳的拉力大小（计算结果保留两位有效数字）；

(2)小车的长度。

Answer 1

【答案】(1)F＝1.2 N (2) x＝0.8m

【解析】

（1）根据机械能守恒定律、动量守恒定律和牛顿第二定律即可求解；（2）根据动量守恒定律和动能定理即可求解。

(1)设物块B刚到达最低点时，速度为v0，物块B自开始释放到运动至最低点过程中，由机械能守恒定律得：

物块B与物块A发生弹性碰撞，设碰后A、B的速度分别为v1、v2

由A、B碰撞前后动量守恒、机械能守恒有：

在A点，由牛顿第二定律有：

联立解得：F＝1.2N

(2)物块A滑到小车右端时的速度与小车的相等，设物块和小车的共同速度大小为v

由动量守恒定律有：

由动能定理得：

联立解得：x＝0.8 m。