题目内容
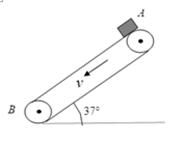
如图所示，一条长为L的细线，上端固定，将它置于一充满匀强电场的空间中，场强大小为E，方向水平向右。已知当细线向右偏离竖直方向的偏角为θ时，带电小球处于平衡状态。求：
⑴小球带电量为多少？
⑵如果使细线向右与竖直方向的偏角由θ增大为β，且自由释放小球，则β为多大时，才能使细线达到竖直位置时，小球的速度又刚好为零？
⑶如果将小球向左方拉成水平，此时线被拉直，自由释放小球后，经多长时间细线又被拉直？
（1）
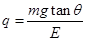（2）β=2θ （3）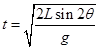
解析试题分析：
（1）小球平衡状态 Eq=mgtanθ,解得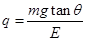
（2）对整个过程由动能定理 mgL(1-cosβ)-EqLsin β="0" ，解得 tanβ/2=tanθ,解得：β=2θ
（3）自由释放后小球作匀加速直线运动到细线又被拉直过程中， 因为 s = 2Lsinθ
而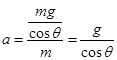
根据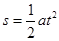
得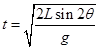
考点：牛顿定律及动能定理。
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
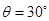的光滑斜面连接，质量m=1.0kg的小滑块从圆弧顶点D由静止释放，已知滑块与水平面间的动摩擦因数
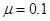，取g=10m／s2．
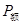=10.0W，赛车的质量m=1.0kg，在水平直轨道上受到的阻力f=2.0N，AB段长L=10.0m，BE的高度差h=1.25m，BE的水平距离x=1.5m。若赛车车长不计，忽略空气阻力，g取10m/s2．
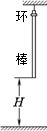
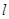的正方形方框，方框内有大小可调、方向竖直向下的匀强磁场，方框左边界的中点有一小孔，恰能让质量为m、带电量为+q的小球b（可视为质点）无阻碍的通过。初始时，小球b静止在小孔处。边界线MN的左侧有一范围足够大的匀强电场区域，电场的电场强度为E，方向水平向左，MN的右侧与方框的左侧间的距离可忽略不计。现有另一质量为
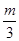、不带电的小球a以速度
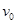正对b球运动。设所有的碰撞均无能量损失和电量的转移，不计一切摩擦，则：
、
；
；
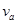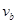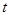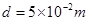，B板中心有小孔O，两板间电势差随时间变化如图乙.
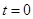时刻，将一质量
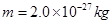，电量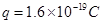
的带正电粒子自O点由静止释放，粒子重力不计．求：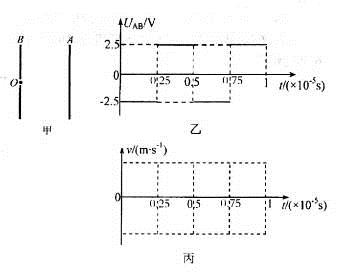 
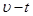图象．(至少画一个周期，标明数据，不必写出计算过程)
。
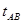