题目内容
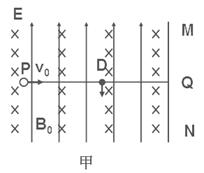
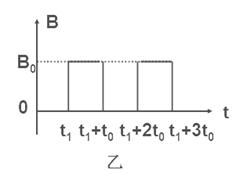
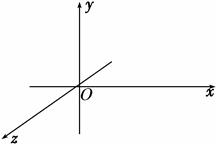
如图所示，Ox、Oy、Oz为相互垂直的坐标轴，Oy轴为竖直方向，整个空间存在竖直向下的匀强磁场，磁感应强度大小为B．现有一质量为m、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出（不计空气阻力，重力加速度为g）．求：
（1）若在整个空间加一匀强电场E1，使小球在xOz平面内做匀速圆周运动，求场强E1；
（2）若在整个空间加一匀强电场E2，使小球沿Ox轴做匀速直线运动，求E2的大小；
（3）若在整个空间加一沿y轴正方向的匀强电场E3，使E3＝3E1，求该小球从坐标原点O抛出后，经过y轴时的坐标y的表达式．
（1）若在整个空间加一匀强电场E1，使小球在xOz平面内做匀速圆周运动，求场强E1；
（2）若在整个空间加一匀强电场E2，使小球沿Ox轴做匀速直线运动，求E2的大小；
（3）若在整个空间加一沿y轴正方向的匀强电场E3，使E3＝3E1，求该小球从坐标原点O抛出后，经过y轴时的坐标y的表达式．
（1）
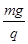方向沿y轴正向 （2）
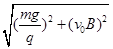（3）y＝
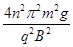(n＝1，2，3……)
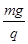方向沿y轴正向 （2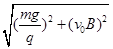） （3）y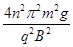＝ (n＝1，2，3……)试题分析：（1）由于小球在磁场中做匀速圆周运动，设轨道半径为r，则
qE1＝mg解得E1＝
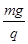（4分）方向沿y轴正向 （1分）
（2）小球做匀速直线运动，受力平衡，则
qE2＝
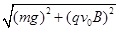（3分）解得E2＝
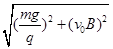（2分）（3）小球在复合场中做螺旋运动，可以分解成水平面内的匀速圆周运动和沿y轴方向的匀加速运动．
做匀加速运动的加速度a＝
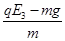＝2g （1分）从原点O到经过y轴时经历的时间t＝nT=
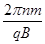（1分）y＝
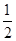at2解得y＝
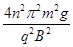(n＝1，2，3……) （3分）
练习册系列答案
相关题目
，磁场为水平方向（图中垂直纸面向外），磁感应强度大小为B；在第二象限分布着沿x轴正向的水平匀强电场，场强大小
。现将放在A点的带电小球由静止释放，则小球需经多少时间才能落到地面（小球所带的电量不变）？
，圆心O′坐标为(-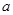
的入射方向为y轴正方向，b的入射方向与y轴正方向夹角为
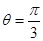。电子a经过磁场偏转后从y轴上的 Q(0，
，匀强电场宽为
。已知电子质量为
、电荷量为
,不计重力及电子间的相互作用。求：
，a）点时，撤去电场，粒子继续运动一段时间后进入一个矩形匀强磁场区域（图中未画出），又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点。已知磁场方向垂直xOy平面（纸面）向里，磁感应强度大小为B，不计粒子的重力。试求：
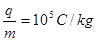，OP间距离为l＝0.3m。全过程不计粒子所受的重力，求：
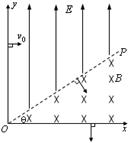
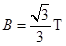，方向垂直于纸面向里．一正离子沿平行于金属板面，从A点垂直于磁场的方向射入平行金属板之间，沿直线射出平行金属板之间的区域，并沿直径CD方向射入圆形磁场区域，最后从圆形区域边界上的F点射出．已知速度的偏向角
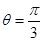，不计离子重力．求：
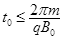且为未知量。求：
