题目内容
3.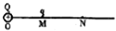 在真空中的O点放一点荷Q=2.0×10-9C,直线MN过O点,OM=30cm,M点放有一点电荷q=4.0×10-10C,静电力常数k=9×109Nm2/C2,如图所示.求:
在真空中的O点放一点荷Q=2.0×10-9C,直线MN过O点,OM=30cm,M点放有一点电荷q=4.0×10-10C,静电力常数k=9×109Nm2/C2,如图所示.求:(1)点荷Q在M点产生的电场强度大小;
(2)若M点的电势比N点的电势高15V,则电荷q从M点移到N点,电势能变化了多少?
分析 (1)已知场源电荷Q的电荷量,知道M点到Q的距离,由点电荷的场强公式E=k$\frac{Q}{{r}^{2}}$可以直接求得Q在M点产生的电场强度大小.
(2)根据电场力做功的公式WMN=qUMN,可直接求得电场力做的功的大小,从而求得电势能的变化量.
解答 解:(1)已知Q=2.0×10-9C,M点到Q的距离为:r=OM=30cm=0.3m
由E=k$\frac{Q}{{r}^{2}}$可得M点的电场强度为:E=9.0×109×$\frac{2.0×1{0}^{-9}}{0.{3}^{2}}$N/C=200N/C;
(2)电荷q从M点移到N点,电场力做的功为:
WMN=qUMN=q(φM-φN)=-4.0×10-10×15J=-6×10-9J
由于电场力做负功,则电荷q从M点移到N点,电势能增加了6×10-9J.
答:
(1)M点的电场强度大小为200N/C;
(2)电荷q从M点移到N点,电势能增加了6×10-9.
点评 本题关键掌握点电荷的场强公式和电场力做的功公式,知道电荷克服电场力做功多少,其电势能就增加多少,掌握住基本内容就可以解决这道题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.下列四个现象中,表明电流间有相互作用力的是( )


| A. | 甲图,置于通电导线附近的小磁针发生偏转 | |
| B. | 乙图,通电导线在磁场中悬线偏离竖直方向 | |
| C. | 丙图,电流方向相同时,导线相互靠近 | |
| D. | 丁图,电流方向相反时,导线相互远离 |
14.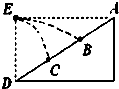 A、D分别是斜面的顶端、底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )
A、D分别是斜面的顶端、底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )
 A、D分别是斜面的顶端、底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )
A、D分别是斜面的顶端、底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )| A. | 球1和球2运动的时间之比为1:2 | |
| B. | 球1和球2动能增加量之比为1:2 | |
| C. | 球1和球2抛出时初速度之比为2$\sqrt{2}$:1 | |
| D. | 球1和球2运动时的加速度之比为1:2 |
11.下列说法中正确的是( )
| A. | 库仑通过扭秤实验确认了真空中两个静止点电荷之间的相互作用规律 | |
| B. | 亚里士多德根据理想斜面实验,提出力不是维持物体运动的原因 | |
| C. | 牛顿发现了万有引力定律,并设计了扭秤测量出了引力常量 | |
| D. | 法拉第通过实验研究发现通电导线能产生磁场 |
18.有一小船正在横渡一条宽为30m的河流,在正对岸下游40m处有一危险水域,假若水流速度为5m/s,为了使小船在危险水域之前到达对岸,那么,小船相对静水的最小速度为( )
| A. | 2m/s | B. | 3m/s | C. | 4m/s | D. | 5m/s |
13.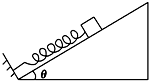 如图所示,在倾角为θ的光滑斜面上有一轻质弹簧,其一端固定在斜面下端的挡板上,另一端与质量为m的物体接触(未连接),物体静止时弹簧被压缩了x0.现用力F缓慢沿斜面向下推动物体,使弹簧在弹性限度内再被压缩2x0后保持物体静止,然后撤去F,物体沿斜面向上运动的最大距离为4.5x0,则在撤去F后到物体上升到最高点的过程中( )
如图所示,在倾角为θ的光滑斜面上有一轻质弹簧,其一端固定在斜面下端的挡板上,另一端与质量为m的物体接触(未连接),物体静止时弹簧被压缩了x0.现用力F缓慢沿斜面向下推动物体,使弹簧在弹性限度内再被压缩2x0后保持物体静止,然后撤去F,物体沿斜面向上运动的最大距离为4.5x0,则在撤去F后到物体上升到最高点的过程中( )
 如图所示,在倾角为θ的光滑斜面上有一轻质弹簧,其一端固定在斜面下端的挡板上,另一端与质量为m的物体接触(未连接),物体静止时弹簧被压缩了x0.现用力F缓慢沿斜面向下推动物体,使弹簧在弹性限度内再被压缩2x0后保持物体静止,然后撤去F,物体沿斜面向上运动的最大距离为4.5x0,则在撤去F后到物体上升到最高点的过程中( )
如图所示,在倾角为θ的光滑斜面上有一轻质弹簧,其一端固定在斜面下端的挡板上,另一端与质量为m的物体接触(未连接),物体静止时弹簧被压缩了x0.现用力F缓慢沿斜面向下推动物体,使弹簧在弹性限度内再被压缩2x0后保持物体静止,然后撤去F,物体沿斜面向上运动的最大距离为4.5x0,则在撤去F后到物体上升到最高点的过程中( )| A. | 物体的机械能守恒 | |
| B. | 弹簧弹力对物体做功的功率一直增大 | |
| C. | 弹簧弹力对物体做的功为4.5mgx0sin θ | |
| D. | 物体从开始运动到速度最大的过程中重力做的功为2mgx0sin θ |
 如图所示的电路中,电路两端的电压为U,三个相同电灯的阻值均为R;
如图所示的电路中,电路两端的电压为U,三个相同电灯的阻值均为R; 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1顺时针运动,一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最后滑块返回传送带的右端,关于这一过程,求:
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1顺时针运动,一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最后滑块返回传送带的右端,关于这一过程,求: