题目内容
一个质量m=0．1 kg的正方形金属框R=O．sΩ，金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AA′重合)，自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合)，设金属框在下滑过程中的速度为v，与此对应的位移为s，那么v2―s图象如图所示，已知匀强磁场方向垂直斜面向上．试问：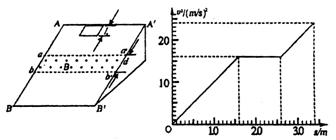
(1)根据v2―s图象所提供的信息，计算出斜面倾角θ和匀强磁场宽度d．
(2)匀强磁场的磁感强度多大?金属框从斜面顶端滑至底端所需的时间为多少?
(3)现用平行斜面沿斜面向上的恒力F1作用在金属框上，使金属框从斜面底端BB′(金属框下边与BB′重合)由静止开始沿斜面向上运动，匀速通过磁场区域后平行斜面沿斜面向上的恒力变为F2，金属框到达斜面顶端(金属框上边与从AA’重合)．试计算恒力F1、F2所做总功的最小值．
(20分)(1)s=0到s=1.6m由公式v2==2a1s，∴该段图线斜率就是线框的加速度。 ∴ a1=5.0m/s2 (2分)根据牛顿第二定律mgsinθ=ma1 θ=30° (2分)(2)线框通过磁场时，v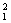
=16,v1=4m/s,此时F安=mg sinθ BL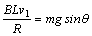
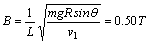(3分)由v2-s图可知，s1=1.6m v0=0 a1=gsinθ 匀加速运动 s2=1.0m v1=4m/s 匀速运动 s3=0.8m 初速v1=4m/s a3=gsinθ 匀加速运动因此，金属框斜面顶端滑至底端所用的时间为t=
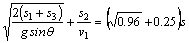(3分)（3）进入磁场前F－mgsinθ=ma 4 在磁场中运动F=masinθ+F安， 由上式得F安= ma4 …………(2分) BL
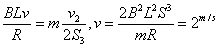所以，a4=2.5m/s2 F安=ma4=0.1×2.5N=0.25N …………(3分)∴最小总功W总=F安×2d+mg(s1+s2+s3)sinθ=1.95J …………(3分)
=16,v1=4m/s,此时F安=mg sinθ BL (3分)由v2-s图可知，s1=1.6m v0=0 a1=gsinθ 匀加速运动 s2=1.0m v1=4m/s 匀速运动 s3=0.8m 初速v1=4m/s a3=gsinθ 匀加速运动因此，金属框斜面顶端滑至底端所用的时间为t= (3分)（3）进入磁场前F－mgsinθ=ma 4 在磁场中运动F=masinθ+F安， 由上式得F安= ma4 …………(2分) BL所以，a4=2.5m/s2 F安=ma4=0.1×2.5N=0.25N …………(3分)∴最小总功W总=F安×2d+mg(s1+s2+s3)sinθ=1.95J …………(3分) 
练习册系列答案
智慧小复习系列答案
相关题目
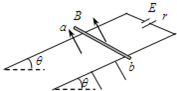如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37°，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直遇导轨所在平面的匀强磁场．金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源．现把一个质量m=0.040kg的导体棒ab放在金属导轨上，导体棒恰好静止．导体棒与金属导轨垂直、且接触良好，导体棒与金属导轨接触的两点间的电阻R0=2.5Ω，金属导轨电阻不计，g取10m/s2．已知sin37°=0.60，cos37°=0.80，求：
（2004?惠州一模）如图所示，质量M=0.8kg的小车静止在光滑的水平面上，左端紧靠竖直墙，在车上左端水平固定着一只弹簧，弹簧右端放一个质量m=0.2kg的滑块，弹簧为原长时，滑块位于C处（滑块可视为质点），车的上表面AC部分为光滑平面，CB部分为粗糙水平面，CB长L=1m，与滑块的摩擦因数μ=0.4，水平向左推动滑块，将弹簧压缩，然后再把滑块从静止释放，在压缩弹簧过程中推力做功2.5J，滑块释放后，将在车上往复运动，最终停在车上某处，设滑块与车的B端碰撞时机械能无损失，g=10m/s2．
