题目内容
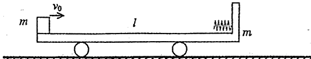 如图所示,在光滑的水平面上有一质量为m,长度为l的小车,小车左端有一质量也是m可视为质点的物块.车子的右壁固定有一个处于锁定状态的压缩轻弹簧(弹簧长度与车长相比可忽略),物块与小车间动摩擦因数为μ,整个系统处于静止.现在给物块一个水平向右的初速度v0,物块刚好能与小车右壁的弹簧接触,此时弹簧锁定瞬间解除,当物块再回到左端时,与小车相对静止.求:
如图所示,在光滑的水平面上有一质量为m,长度为l的小车,小车左端有一质量也是m可视为质点的物块.车子的右壁固定有一个处于锁定状态的压缩轻弹簧(弹簧长度与车长相比可忽略),物块与小车间动摩擦因数为μ,整个系统处于静止.现在给物块一个水平向右的初速度v0,物块刚好能与小车右壁的弹簧接触,此时弹簧锁定瞬间解除,当物块再回到左端时,与小车相对静止.求:(1)物块的初速度v0;
(2)在上述整个过程中小车相对地面的位移.
分析:(1)物块从左端向右运动到小车右壁的过程中,物块与车组成的系统动量守恒,系统减少的机械能等于克服摩擦力做的功,由动量守恒定律与能量守恒定律可以求出物块的初速度.
(2)在整个过程中,系统动量守恒,由动量守恒定律、能量守恒定律、运动学公式可以求出小车的位移.
(2)在整个过程中,系统动量守恒,由动量守恒定律、能量守恒定律、运动学公式可以求出小车的位移.
解答:解:(1)物块在小车上运动到右壁时,
小车与物块的共同速度设为v,
由动量守恒定律得:mv0=2mv ①,
由能量守恒定律得:
m
-
(2m)v2=μmgl ②,
解得:v0=2
; ③
(2)弹簧锁定解开瞬间,设小车速度为v车,物块速度为v物,
最终物块与小相对静止时,共同速度为v′,
由动量守恒定律得:mv0=2mv′④,解得:v′=
,
由能量守恒定律得:
m
+
m
-
(2m)v′2=μmgl ⑤,
解得:
,
(不合题意舍去) ⑥
在物块相对车向右运动过程中,小车向右作加速运动,
加速度a=μg,速度由0增加到
,小车的位移S1=
=
⑦,
物体相对小车向左运动过程中,小车作减速运动,加速度a′=-μg,
速度由v0减小为
,位移S2=
=
⑧,
整个过程中,小车位移:S=S1+S2=2l.
答:(1)物块的初速度为2
;
(2)在上述整个过程中小车相对地面的位移为2l.
小车与物块的共同速度设为v,
由动量守恒定律得:mv0=2mv ①,
由能量守恒定律得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解得:v0=2
| ugl |
(2)弹簧锁定解开瞬间,设小车速度为v车,物块速度为v物,
最终物块与小相对静止时,共同速度为v′,
由动量守恒定律得:mv0=2mv′④,解得:v′=
| v0 |
| 2 |
由能量守恒定律得:
| 1 |
| 2 |
| v | 2 车 |
| 1 |
| 2 |
| v | 2 物 |
| 1 |
| 2 |
解得:
|
|
在物块相对车向右运动过程中,小车向右作加速运动,
加速度a=μg,速度由0增加到
| v0 |
| 2 |
(
| ||
| 2a |
| l |
| 2 |
物体相对小车向左运动过程中,小车作减速运动,加速度a′=-μg,
速度由v0减小为
| v0 |
| 2 |
(
| ||||
| 2a′ |
| 3l |
| 2 |
整个过程中,小车位移:S=S1+S2=2l.
答:(1)物块的初速度为2
| μgl |
(2)在上述整个过程中小车相对地面的位移为2l.
点评:分析清楚物块与小车的运动过程是正确解题的关键,分析清楚物体的运动过程、应用动量守恒定律、能量守恒定律、运动学公式即可正确解题.

练习册系列答案
相关题目
 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( )
如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
