题目内容
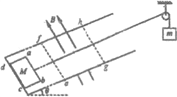
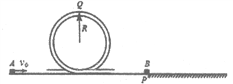
【题目】如图所示,带有圆管轨道的长轨道水平固定,圆管竖直(管内直径可以忽略),底端分别与两侧的直轨道相切,圆管轨道的半径R=0.5m, P点左侧轨道(包括圆管)光滑,右侧轨道粗糙。质量m=lkg的物块A以![]() 的速度滑入圆管,滑过最高点Q,与直轨上P处静止的质量M=3kg的物块B发生碰撞(碰撞时间极短),物块B与粗燥轨道的动摩擦因数
的速度滑入圆管,滑过最高点Q,与直轨上P处静止的质量M=3kg的物块B发生碰撞(碰撞时间极短),物块B与粗燥轨道的动摩擦因数![]() ,(A、B视为质点,重力加速度g取lOm/s2),求:
,(A、B视为质点,重力加速度g取lOm/s2),求:
(1)物块A滑过Q点时受到管壁弹力的大小F。
(2)若碰后物块B在粗糙轨道上滑行6m就停下了,请判断物块A能否再次滑过圆管的最高点Q。
【答案】(1)142N (2)能
【解析】(1)对滑块A,上滑过程中,根据机械能守恒定律: ![]()
在最高点Q,根据牛顿定律: ![]()
联立可知:F=142N
(2)AB碰撞过程,由动量守恒: ![]()
对物块B,根据动能定理: ![]()
联立解得: ![]()
![]()
对物块A,假设能滑过最高点Q,根据机械能守恒定律: ![]()
解得:v4=2m/s>0,
故能滑过最高点Q.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目