题目内容
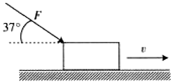
如 图(a),AB为光滑水平面,BC为倾角α=30°的光滑固定斜面,两者在B处平滑连接.质量m=1.6kg的物体,受到与水平方向成θ=37°斜向上拉力F的作用,从A点开始运动,到B点时撤去F,物体冲上光滑斜面.物体在运动过程中的v-t图象如图(b)所示.求:
图(a),AB为光滑水平面,BC为倾角α=30°的光滑固定斜面,两者在B处平滑连接.质量m=1.6kg的物体,受到与水平方向成θ=37°斜向上拉力F的作用,从A点开始运动,到B点时撤去F,物体冲上光滑斜面.物体在运动过程中的v-t图象如图(b)所示.求:
(1)AB段的长度;
(2)拉力F的大小;
(3)物体冲上斜面的最大距离.
 图(a),AB为光滑水平面,BC为倾角α=30°的光滑固定斜面,两者在B处平滑连接.质量m=1.6kg的物体,受到与水平方向成θ=37°斜向上拉力F的作用,从A点开始运动,到B点时撤去F,物体冲上光滑斜面.物体在运动过程中的v-t图象如图(b)所示.求:
图(a),AB为光滑水平面,BC为倾角α=30°的光滑固定斜面,两者在B处平滑连接.质量m=1.6kg的物体,受到与水平方向成θ=37°斜向上拉力F的作用,从A点开始运动,到B点时撤去F,物体冲上光滑斜面.物体在运动过程中的v-t图象如图(b)所示.求:(1)AB段的长度;
(2)拉力F的大小;
(3)物体冲上斜面的最大距离.
(1)AB段做匀加速直线运动,有:sAB=
×2×5m=5m.
(2)物体做匀加速直线运动的加速度为:a1=
=2.5m/s2,
根据牛顿第二定律得:Fcos37°=ma1,
得:F=
=
=5N.
(3)物体在斜面上上滑的加速度大小为:a2=
=gsinα=5m/s2,
则物体冲上斜面的最大距离为:x=
=
=2.5m.
答:(1)ABAB段的长度为5m;
(2)拉力F的大小为5N;
(3)物体冲上斜面的最大距离为2.5m.
| 1 |
| 2 |
(2)物体做匀加速直线运动的加速度为:a1=
| 5 |
| 2 |
根据牛顿第二定律得:Fcos37°=ma1,
得:F=
| ma1 |
| cos37° |
| 1.6×2.5 |
| 0.8 |
(3)物体在斜面上上滑的加速度大小为:a2=
| mgsinα |
| m |
则物体冲上斜面的最大距离为:x=
| v2 |
| 2a2 |
| 25 |
| 10 |
答:(1)ABAB段的长度为5m;
(2)拉力F的大小为5N;
(3)物体冲上斜面的最大距离为2.5m.

练习册系列答案
相关题目