题目内容
17. 如图所示,竖直轻弹簧下端固定在水平地面上,一小球从轻弹簧正上方某一高度处自由落下,并将弹簧压缩,直到小球的速度减为零.对于小球和轻弹簧的系统,在小球开始与弹簧接触到小球速度变为零的过程中,有( )
如图所示,竖直轻弹簧下端固定在水平地面上,一小球从轻弹簧正上方某一高度处自由落下,并将弹簧压缩,直到小球的速度减为零.对于小球和轻弹簧的系统,在小球开始与弹簧接触到小球速度变为零的过程中,有( )| A. | 小球的动能与重力势能之和越来越小,小球的动能与弹性势能之和越来越小 | |
| B. | 小球的动能与重力势能之和越来越小,小球的动能与弹性势能之和越来越大 | |
| C. | 小球的动能与重力势能之和越来越大,小球的动能与弹性势能之和越来越大 | |
| D. | 小球的动能与重力势能之和越来越大,小球的动能与弹性势能之和越来越小 |
分析 小球、弹簧和地球组成的系统机械能守恒,根据弹性势能与弹簧形变量的关系可以判断弹性势能的变化,根据高度变化可以确认重力势能的变化.由系统的机械能守恒分析.
解答 解:因为整个过程中,只有重力和弹簧的弹力做功,小球、弹簧和地球组成的系统的机械能守恒,但对单个物体小球机械能不守恒,根据系统的机械能守恒得知:小球的机械能减小量等于弹簧弹性势能的增加量,小球接触弹簧至弹簧压缩最低点的过程中弹簧的形变量越来越大,弹性势能也越来越大,所以小球的动能和重力势能的总和越来越小,根据系统的机械能守恒得小球的动能和弹性势能的总和变化量等于小球的重力势能减小变化量.小球的重力势能减小,所以小球的动能和弹性势能的总和越来越大.故ACD错误,B正确.
故选:B.
点评 掌握机械能守恒的条件,是解决问题的关键,注意区分系统的机械能守恒和单个物体机械能守恒的区别.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列说法中正确的是( )
| A. | 重心一定在物体上 | |
| B. | 相互接触的物体间一定有弹力 | |
| C. | 不受到弹力的物体不会受到摩擦力 | |
| D. | 摩擦力的方向一定与物体运动方向相反 |
5.两相同金属小球A、B所带电荷量分别为+Q、+3Q,固定于相距为2r的两点,此时A、B间库仑力大小为F.若将小球A、B相互接触后,固定于相距为r的另外两点,则此时A、B间库仑力的大小为(两带电球均视为点电荷)( )
| A. | $\frac{1}{3}$F | B. | $\frac{4}{3}$F | C. | $\frac{1}{16}$F | D. | $\frac{16}{3}$F |
2.我国志愿者王跃曾与俄罗斯志愿者一起进行“火星500”的实验活动.假设王跃登陆火星后,测得火星的半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$.已知地球表面的重力加速度是g,地球的半径为R,王跃在地面上能向上竖直跳起的最大高度是h,忽略自转的影响,下列说法正确的是( )
| A. | 火星的密度为$\frac{2g}{3πGR}$ | |
| B. | 火星表面的重力加速度是$\frac{2g}{9}$ | |
| C. | 火星的第一宇宙速度与地球的第一宇宙速度之比为$\frac{\sqrt{2}}{3}$ | |
| D. | 王跃以与在地球上相同的初速度在火星上起跳后,能达到的最大高度是$\frac{9h}{2}$ |
9.下列关于质点的说法中,正确的是( )
| A. | 质点是一个理想化的模型,实际并不存在 | |
| B. | 凡是质量轻、体积小的物体,都可看作质点 | |
| C. | 各部分运动状态完全一致的物体一定可视为质点 | |
| D. | 如果物体的形状和大小在所研究的问题中属于次要因素,就可以把物体看作质点 |
6. 在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
 在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )| A. | 质量大的卫星,其加速度也大 | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动到位置B所需时间为$\frac{πr}{3R}\sqrt{\frac{r}{R}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |
7.某物体做匀变速直线运动,加速度大小为6m/s2,那么在任意1s内( )
| A. | 此物体的末速度一定等于初速度的6倍 | |
| B. | 此物体任意1 s的初速度与前1 s末的速度相等 | |
| C. | 此物体在每1 s内的速度变化大小为6 m/s | |
| D. | 此物体在任意1 s内的末速度比初速度大6 m/s |
 如图是一种配有小型风力发电机和光电池的新型路灯,其功率P=120W.该风力发电机的线圈由风叶直接带动,其产生的电流可视为正弦交流电.已知风叶的半径r=1m,风能的利用效率η1=4%,风力发电机的线圈共有N=200匝,磁场的磁感应强度B=0.1T,线圈的面积S1=0.2m2,空气的密度ρ=1.3kg/m3.太阳垂直照射到地面上单位面积上的功率P0=1kW,如果光电池板垂直太阳光方向的平均受光面积为S=1m2,光能的利用效率为η2=20%,π取3,结果均保留2位有效数字.
如图是一种配有小型风力发电机和光电池的新型路灯,其功率P=120W.该风力发电机的线圈由风叶直接带动,其产生的电流可视为正弦交流电.已知风叶的半径r=1m,风能的利用效率η1=4%,风力发电机的线圈共有N=200匝,磁场的磁感应强度B=0.1T,线圈的面积S1=0.2m2,空气的密度ρ=1.3kg/m3.太阳垂直照射到地面上单位面积上的功率P0=1kW,如果光电池板垂直太阳光方向的平均受光面积为S=1m2,光能的利用效率为η2=20%,π取3,结果均保留2位有效数字.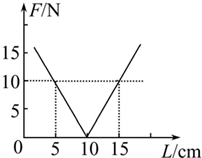 某物理兴趣小组的同学在研究弹簧弹力的时候,测得弹力的大小F和弹簧长度L的关系如图所示,则由图线可知:
某物理兴趣小组的同学在研究弹簧弹力的时候,测得弹力的大小F和弹簧长度L的关系如图所示,则由图线可知: