题目内容
如图所示,在竖直面内有两平行金属导轨AB、CD,间距为L ,金属棒ab可在导轨上无摩擦地滑动。棒与导轨垂直,并接触良好,它们的电阻均可不计。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B,导轨右边与电路连接。电路中的三个定值电照R1、R2、R3阻值分别为2R、R和0.5R。在BD间接有一水平放置的平行板电容器C,极板间距离为d 。(1)当ab以速度v0匀速向右运动时,电容器中质量为m的带电微粒恰好静止。试判断微粒的带电性质,及带电量的大小。
(2)当AB棒以某一速度沿导轨匀速运动时,发现带电微粒从两极板中间由静止开始向下运动,历时t=2×10-2 s到达下极板,已知电容器两极板间距离d=6×10-3m,求ab棒的速度大小和方向。(g=10m/s2)
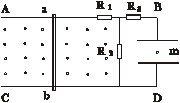
解析:(1)棒匀速向左运动,感应电流为顺时针方向,电容器上板带正电.因微粒受力平衡,电场力向上,场强方向向下,则微粒带负电。 设微粒带电量大小为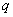 ,由平衡条件知:
,由平衡条件知: 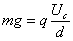 ①-----------(2分) 对R1、R2和金属棒构成的回路,由欧姆定律可得
①-----------(2分) 对R1、R2和金属棒构成的回路,由欧姆定律可得 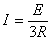 ②
②  ③-----------(2分) 由法拉第电磁感应定律可得
③-----------(2分) 由法拉第电磁感应定律可得 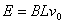 ④ 由以上各式求得
④ 由以上各式求得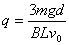 ⑤-----------(2分) (2)因带电微粒从极板中间开始向下作初速度为零的匀加速运动,由运动学公式得:
⑤-----------(2分) (2)因带电微粒从极板中间开始向下作初速度为零的匀加速运动,由运动学公式得: 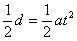 ⑥ 得
⑥ 得 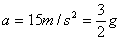 >
>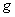 ⑦-----------(1分) 可见带电微粒受到的电场力向下,所以
⑦-----------(1分) 可见带电微粒受到的电场力向下,所以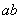 棒应向右运动,设此时极板间电压为
棒应向右运动,设此时极板间电压为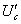 ,由牛顿第二定律得
,由牛顿第二定律得 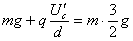 ⑧ 出⑤和⑧得
⑧ 出⑤和⑧得 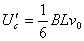 -----------(2分) 设棒ab运动速度为
-----------(2分) 设棒ab运动速度为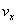 ,则电动势
,则电动势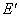 =
=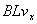 ,由欧姆定律得
,由欧姆定律得 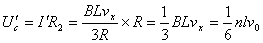 则
则 ,即棒运动速度大小应为原来速度的一半 -----------(3分)思路点拔:这是一道力、电磁相结合的题目,涉及的知识点很多。解这类题的思路是:先根据法拉第电磁感应定律确定电源,看清电路的结构,画出等效电路图,计算电容器的电压,再判断带电粒子的运动;或者刚好反过来,逆着这条思路求解问题。
,即棒运动速度大小应为原来速度的一半 -----------(3分)思路点拔:这是一道力、电磁相结合的题目,涉及的知识点很多。解这类题的思路是:先根据法拉第电磁感应定律确定电源,看清电路的结构,画出等效电路图,计算电容器的电压,再判断带电粒子的运动;或者刚好反过来,逆着这条思路求解问题。

练习册系列答案
相关题目
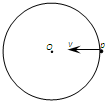 如图所示,在竖直面内有一个圆轨道,圆心为O.P为轨道上与O等高的最右端位置,一小球以某一初速度从p点水平向左抛出,落在圆轨道上的某一点,忽略一切阻力和能量损耗,则下列说法正确的是( )
如图所示,在竖直面内有一个圆轨道,圆心为O.P为轨道上与O等高的最右端位置,一小球以某一初速度从p点水平向左抛出,落在圆轨道上的某一点,忽略一切阻力和能量损耗,则下列说法正确的是( )| A、小球速度合适,球可能垂直撞在圆轨道上 | B、小球初速度合适,位移大小等于直径 | C、初速度越大,落到圆轨道上的时间越长 | D、小球初速度合适,落在O点正下方的圆周上时间最长 |
 如图所示:在竖直面内固定着一个光滑
如图所示:在竖直面内固定着一个光滑 (2011?海淀区模拟)如图所示,在竖直面内有一以O点为圆心的圆,AB、CD分别为这个圆沿竖直和水平方向的直径,该圆处于静电场中.将带负电荷的小球从O点以相同的动能分别沿竖直平面向不同方向射出,小球会沿圆所在平面运动并经过圆周上不同的点.已知小球从O点分别到A、B两点的过程中电场力对它做的功相同,小球到达D点时的电势能大于它在圆周上其他各点时的电势能.若小球只受重力和电场力的作用,则下列说法中正确的是( )
(2011?海淀区模拟)如图所示,在竖直面内有一以O点为圆心的圆,AB、CD分别为这个圆沿竖直和水平方向的直径,该圆处于静电场中.将带负电荷的小球从O点以相同的动能分别沿竖直平面向不同方向射出,小球会沿圆所在平面运动并经过圆周上不同的点.已知小球从O点分别到A、B两点的过程中电场力对它做的功相同,小球到达D点时的电势能大于它在圆周上其他各点时的电势能.若小球只受重力和电场力的作用,则下列说法中正确的是( ) 如图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接.A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧.两滑块从弧形轨道上的某一高度由静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动恰能通过轨道最高点.已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度h=0.80m,重力加速度g取10m/s2,空气阻力可忽略不计.求:
如图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接.A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧.两滑块从弧形轨道上的某一高度由静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动恰能通过轨道最高点.已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度h=0.80m,重力加速度g取10m/s2,空气阻力可忽略不计.求: 如图所示,在竖直面内有固定轨道ABCDE,其中BC是半径为R的四分之一圆弧轨道,AB(AB>R)是竖直轨道,CE是足够长的水平轨道,CD>R.AB与BC相切于B点,BC与CE相切于C点,轨道的AD段光滑,DE段粗糙且足够长.一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q(视为质点),将轻杆锁定在图示位置,此位置Q与B等高.现解除锁定释放轻杆,轻杆将沿轨道下滑,Q球经过D点后,沿轨道继续滑行了3R而停下.重力加速度为g.求:
如图所示,在竖直面内有固定轨道ABCDE,其中BC是半径为R的四分之一圆弧轨道,AB(AB>R)是竖直轨道,CE是足够长的水平轨道,CD>R.AB与BC相切于B点,BC与CE相切于C点,轨道的AD段光滑,DE段粗糙且足够长.一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q(视为质点),将轻杆锁定在图示位置,此位置Q与B等高.现解除锁定释放轻杆,轻杆将沿轨道下滑,Q球经过D点后,沿轨道继续滑行了3R而停下.重力加速度为g.求: