题目内容
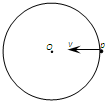如图所示，在竖直面内有一个圆轨道，圆心为O．P为轨道上与O等高的最右端位置，一小球以某一初速度从p点水平向左抛出，落在圆轨道上的某一点，忽略一切阻力和能量损耗，则下列说法正确的是（ ）| A、小球速度合适，球可能垂直撞在圆轨道上 | B、小球初速度合适，位移大小等于直径 | C、初速度越大，落到圆轨道上的时间越长 | D、小球初速度合适，落在O点正下方的圆周上时间最长 |
分析：小球抛出后做平抛运动，由平抛运动的规律及圆的性质可确定各项是否正确．
解答：解：A、若小球垂直打在圆轨道上，则速度方向的反向延长线应交于圆心；而于平抛运动的规律可知，速度方向的反向延长线应交于水平位移的中点；但打在圆上只能打在初速度方向的下方，不可能出现水平位移为直径的情况；故A错误；
B、由A的分析可知，小球打在圆上的位移只能小于直径；故B错误；
C、下落时间取决于小球的高度；故速度越大，小球下落时间越短，故C错误；
D、小球落在O点正下方时，小球下落的高度最大，故下落时间最长；故D正确；
故选：D．
B、由A的分析可知，小球打在圆上的位移只能小于直径；故B错误；
C、下落时间取决于小球的高度；故速度越大，小球下落时间越短，故C错误；
D、小球落在O点正下方时，小球下落的高度最大，故下落时间最长；故D正确；
故选：D．
点评：本题考查平抛运动的规律，注意结合圆的性质，并能正确应用平抛运动的结论进行分析．
练习册系列答案
阅读快车系列答案
相关题目
如图所示：在竖直面内固定着一个光滑
（2011?海淀区模拟）如图所示，在竖直面内有一以O点为圆心的圆，AB、CD分别为这个圆沿竖直和水平方向的直径，该圆处于静电场中．将带负电荷的小球从O点以相同的动能分别沿竖直平面向不同方向射出，小球会沿圆所在平面运动并经过圆周上不同的点．已知小球从O点分别到A、B两点的过程中电场力对它做的功相同，小球到达D点时的电势能大于它在圆周上其他各点时的电势能．若小球只受重力和电场力的作用，则下列说法中正确的是（ ）
如图所示，在竖直面内有一个光滑弧形轨道，其末端水平，且与处于同一竖直面内光滑圆形轨道的最低端相切，并平滑连接．A、B两滑块（可视为质点）用轻细绳拴接在一起，在它们中间夹住一个被压缩的微小轻质弹簧．两滑块从弧形轨道上的某一高度由静止滑下，当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开，弹簧迅速将两滑块弹开，其中前面的滑块A沿圆形轨道运动恰能通过轨道最高点．已知圆形轨道的半径R=0.50m，滑块A的质量mA=0.16kg，滑块B的质量mB=0.04kg，两滑块开始下滑时距圆形轨道底端的高度h=0.80m，重力加速度g取10m/s2，空气阻力可忽略不计．求：
如图所示，在竖直面内有固定轨道ABCDE，其中BC是半径为R的四分之一圆弧轨道，AB（AB＞R）是竖直轨道，CE是足够长的水平轨道，CD＞R．AB与BC相切于B点，BC与CE相切于C点，轨道的AD段光滑，DE段粗糙且足够长．一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q（视为质点），将轻杆锁定在图示位置，此位置Q与B等高．现解除锁定释放轻杆，轻杆将沿轨道下滑，Q球经过D点后，沿轨道继续滑行了3R而停下．重力加速度为g．求：