题目内容
9.光滑水平面上排列着三个等大的球心共线的弹性小球,质量分别为m1、m2、m3.现给1号球一个水平速度v0.于是,1号球与2号球、2号球与3号球依次发生碰撞,碰撞过程无机械能守恒.(即完全弹性碰撞)①求最终三个球的速度.(每两个球只发生一次碰撞)
②若1、3号球质量m1,m3已知,要3号球碰后速度最大,则2号球质量m2为多大.

分析 (1)任意两球碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出球的速度.
(2)根据3号球的速度表达式应用数学知识求出何时它的速度最大.
解答 解:(1)m1、m2碰撞过程系统动量守恒,以m1的初速度方向为正方向,
由动量守恒定律得:m1v0=m1v1+m2v,
由机械能守恒定律得:$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v2,
解得:v1=$\frac{{(m}_{1}-{m}_{2}){v}_{0}}{{m}_{1}+{m}_{2}}$,v=$\frac{2{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}}$;
m2、m3碰撞过程系统动量守恒,以m2的初速度方向为正方向,
由动量守恒定律得:m2v=m2v2+m3v3,
由机械能守恒定律得:$\frac{1}{2}$m2v2=$\frac{1}{2}$m2v22+$\frac{1}{2}$m3v32,
解得:v2=$\frac{2{m}_{1}({m}_{2}-{m}_{3}){v}_{0}}{({m}_{1}+{m}_{2})({m}_{2}+{m}_{3})}$,v3=$\frac{4{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}+{m}_{3}+\frac{{m}_{1}{m}_{3}}{{m}_{2}}}$;
(2)由(1)可知,v3=$\frac{4{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}+{m}_{3}+\frac{{m}_{1}{m}_{3}}{{m}_{2}}}$,
当m2=$\frac{{m}_{1}{m}_{3}}{{m}_{2}}$时,v3的值最大,m2=$\sqrt{{m}_{1}{m}_{3}}$;
答:(1)最终三个球的速度大小分别为$\frac{{(m}_{1}-{m}_{2}){v}_{0}}{{m}_{1}+{m}_{2}}$、$\frac{2{m}_{1}({m}_{2}-{m}_{3}){v}_{0}}{({m}_{1}+{m}_{2})({m}_{2}+{m}_{3})}$、$\frac{4{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}+{m}_{3}+\frac{{m}_{1}{m}_{3}}{{m}_{2}}}$;
(2)2号球质量m2为$\sqrt{{m}_{1}{m}_{3}}$时3号球碰后速度最大.
点评 本题考查了求球的速度,分析清楚球的运动过程,应用动量守恒定律与机械能守恒定律即可正确解题.

 智慧小复习系列答案
智慧小复习系列答案| A. | 速度一定等于零 | B. | 速度一定不等于零 | ||
| C. | 加速度一定等于零 | D. | 加速度一定不等于零 |
 公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速度为vc时,汽车恰好没有向公路内外两侧滑动的趋势,则在该弯道处,( )
公路急转弯处通常是交通事故多发地带.如图,某公路急转弯处是一圆弧,当汽车行驶的速度为vc时,汽车恰好没有向公路内外两侧滑动的趋势,则在该弯道处,( )| A. | 汽车所受重力和支持力是一对平衡力 | |
| B. | 车速只要低于vc,车辆便一定会向内侧滑动 | |
| C. | 车速只要高于vc,车辆便一定会向外侧滑动 | |
| D. | 当路面结冰时,与未结冰时相比,vc的值不变 |
 如图所示,真空中O点有一点电荷,在经产生的电场中有a,b两点,a点的场强大小为Ea,方向与ab连线成60°角,b点的场强大小为Eb,方向与ab连线成30°角,若将同一试探电荷分别放在a,b两点受电场力大小分别为Fa、Fb,则关于试探电荷在a、b两点电场力的大小关系,以下结论正确的是( )
如图所示,真空中O点有一点电荷,在经产生的电场中有a,b两点,a点的场强大小为Ea,方向与ab连线成60°角,b点的场强大小为Eb,方向与ab连线成30°角,若将同一试探电荷分别放在a,b两点受电场力大小分别为Fa、Fb,则关于试探电荷在a、b两点电场力的大小关系,以下结论正确的是( )| A. | Fa=3Fb | B. | Fa=$\sqrt{3}$Fb | C. | Fa=$\frac{\sqrt{3}}{3}$Fb | D. | Fa=$\frac{1}{3}$Fb |

| A. | 弹簧拉伸至最长时,A、B两物体和弹簧组成的系统总动量为0 | |
| B. | 弹簧拉伸至最长时,弹簧的弹性势能与初始时相同 | |
| C. | 弹簧拉伸至最长时,弹簧的弹性势能小于初始时的弹性势能 | |
| D. | 弹簧拉伸至最长时,A、B、C和弹簧组成的系统总动量不为0 |
 如图所示,轻绳的一端系在质量为m的物体上,另一端系在轻质圆环上,圆环套在粗糙水平杆MN上,先用水平力F拉绳上一点,使物体处于图中实线位置,然后改变F的大小使其缓慢下降到图中虚线位置,圆环仍在原来的位置不动,则在这一过程中,水平力F、环与杆的摩擦力f和环对杆的压力N以及轻绳对环的拉力T的大小变化情况是( )
如图所示,轻绳的一端系在质量为m的物体上,另一端系在轻质圆环上,圆环套在粗糙水平杆MN上,先用水平力F拉绳上一点,使物体处于图中实线位置,然后改变F的大小使其缓慢下降到图中虚线位置,圆环仍在原来的位置不动,则在这一过程中,水平力F、环与杆的摩擦力f和环对杆的压力N以及轻绳对环的拉力T的大小变化情况是( )| A. | F逐渐减小,f逐渐减小,N保持不变,T逐渐减小 | |
| B. | F逐渐增大,f逐渐增大,N保持减小,T逐渐减小 | |
| C. | F逐渐增大,f保持不变,N逐渐增大,T逐渐增大 | |
| D. | F逐渐减小,f逐渐减小,N保持不变,T保持不变 |
 如图1在粗糙的水平面上有一个3kg的物体,在0~4s内受水平力拉力F的作用,在4~10s内撤去水平拉力F,其v-t图象如图2所示.求:
如图1在粗糙的水平面上有一个3kg的物体,在0~4s内受水平力拉力F的作用,在4~10s内撤去水平拉力F,其v-t图象如图2所示.求: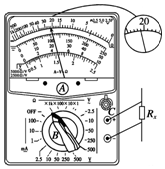 如图所示为多用电表示意图.其中A、B、C为三个可调节的部件.某同学在实验室中用它测量一阻值约为几百欧的电阻.他测量的操作步骤如下:
如图所示为多用电表示意图.其中A、B、C为三个可调节的部件.某同学在实验室中用它测量一阻值约为几百欧的电阻.他测量的操作步骤如下: