Question

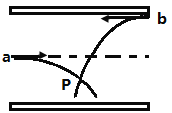
【题目】如图所示，不导电的平板小车C足够长，上表面光滑，放在光滑水平面上，车的右端有挡板(挡板固定在车上)，车的质量(包括挡板) ，今在静止的平板车上放一个带电量＋q、质量为的小物块A，与挡板的距离为2L，绝缘小物块B（不带电）的质量放在A和挡板的正中央，现在整个空间加上一个水平向右的匀强电场、场强大小为，物块A由静止开始向右运动，与B发生的是弹性碰撞，且B以一定速度沿平板向右与C车的挡板相碰，碰后小车的速度等于碰前物块B速度的二分之一．求：

（1）A第一次和B相碰后A的速度大小和方向．

（2）A第二次和B相碰前A的速度大小．

（3）从B第一次与C车的挡板相碰到A第二次与B相碰的时间内，电场力对A做了多少功？

Answer 1

【答案】（1），方向向左；（2）；（3）.

【解析】试题分析：（1）A与B碰撞前只有电场力做功，由动能定理求出碰前A的速度；A与B发生弹性碰撞，由动量守恒和能量守恒即可求解；（2）B与C发生碰撞，由动量守恒可求出碰后B的速度，由动能定理求A再次与B碰前的速度；（3）在B向右做匀速运动与C碰撞的这段时间内，A先向左做减速运动，再向右做匀加速运动，由此求A运动的位移，再根据电场力做功的公式求电场力做的功.

（1）A与B碰撞前，只有电场力做功

由动能定理得：

解得：

A与B的碰撞为弹性碰撞，故动量能量均守恒：

由动量守恒得：

由能量守恒得：

联立解得：

即：A的速度大小为，方向向左

（2）碰后，B向右做匀速直线运动，与C相碰

B与C碰撞过程中由动量守恒得：

又代入上式得：

说明B停在最右端，则A要与B发生第二次碰撞，A要再向右运动的距离为L

则对A分析，由动能定理： ，解得：

即：A第二次碰B前的速度为

（3）对B分析：匀速运动时间为

对A分析：

则有：

则

所以电场力对A做的功为：