题目内容
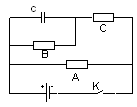
【题目】如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平。设平面内存在沿x轴正方向的恒定风力。一小球从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4 m/s,不计空气阻力,到达最高点的位置如图中M点所示(坐标格为正方形,g取10 m/s2)求:
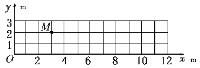
(1)小球在M点的速度v1;
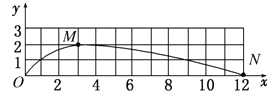
(2)在图中定性画出小球的运动轨迹并标出小球落回x轴时的位置N;
(3)小球到达N点的速度v2的大小。
【答案】(1)6 m/s(2)位置N的坐标为(12,0)(3)![]()
【解析】
试题分析:(1)设正方形的边长为s0。
竖直方向做竖直上抛运动,v0=gt1;![]()
水平方向做匀加速直线运动, ![]()
解得v1=6 m/s。
(2)由竖直方向的对称性可知,小球再经过t1到x轴,水平方向做初速度为零的匀加速直线运动,所以回到x轴时落到x=12处,位置N的坐标为(12,0)。
(3)到N点时竖直分速度大小为v0=4 m/s,
水平分速度vx=a水平tN=2v1=12 m/s,
故![]() 。
。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
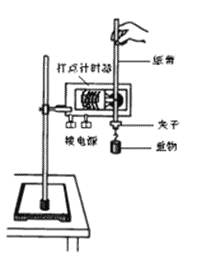
【题目】某同学用如图所示的装置来研究自由落体运动.
(1)下列有关操作的叙述正确的是( )
A.安装打点计时器时要注意让上下限位孔在同一竖直线上 |
B.将打点计时器与直流低压电源连接 |
C.释放纸带时应尽量让重物靠近打点计时器 |
D.应先释放纸带,然后接通电源 |
(2)实验得到一条纸带,测得各点之间的距离如图所示.已知电源频率为50Hz 。从该纸带可知,重物是做_______(选填“匀速”、“匀变速”、 “非匀变速”)直线运动,加速度大小a=________m/s2(保留三位有效数字)。