题目内容
8. 如图所示,长为L的导体棒原来不带电,现将一带电量为Q的点电荷放在距棒左端 R处,当达到静电平衡后,棒上感应电荷在棒内距离左端$\frac{L}{4}$处产生的场强大小等于$\frac{kQ}{(\frac{L}{4}+R)^{2}}$.
如图所示,长为L的导体棒原来不带电,现将一带电量为Q的点电荷放在距棒左端 R处,当达到静电平衡后,棒上感应电荷在棒内距离左端$\frac{L}{4}$处产生的场强大小等于$\frac{kQ}{(\frac{L}{4}+R)^{2}}$.
分析 当棒达到静电平衡后,棒内各点的合场强为零,即感应电荷产生的电场强度与+q产生的电场强度大小相等、方向相反,根据静电平衡的特点和点电荷场强公式E=k$\frac{Q}{{r}^{2}}$结合求解.
解答 解:水平导体棒当达到静电平衡后,棒上感应电荷中点P处产生的场强大小与点电荷+q在该处产生的电场强度大小相等,方向相反.
则棒上感应电荷在棒内距离左端$\frac{L}{4}$处产生的场强大小为:E=$\frac{kQ}{(\frac{L}{4}+R)^{2}}$,
故答案为:$\frac{kQ}{(\frac{L}{4}+R)^{2}}$.
点评 感应带电的本质是电荷的转移,当金属导体处于电场时会出现静电平衡现象,关键要理解并掌握静电平衡的特点.

练习册系列答案
相关题目
18.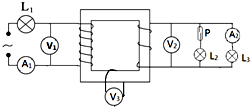 如图所示电路中,电流表和电压表均是理想交流电表,变压器是理想变压器.P处有一个与灯泡L2串联的干簧管,原来P处没有磁场.现在让条形磁铁的一端靠近P处,则以下说法正确的是( )
如图所示电路中,电流表和电压表均是理想交流电表,变压器是理想变压器.P处有一个与灯泡L2串联的干簧管,原来P处没有磁场.现在让条形磁铁的一端靠近P处,则以下说法正确的是( )
 如图所示电路中,电流表和电压表均是理想交流电表,变压器是理想变压器.P处有一个与灯泡L2串联的干簧管,原来P处没有磁场.现在让条形磁铁的一端靠近P处,则以下说法正确的是( )
如图所示电路中,电流表和电压表均是理想交流电表,变压器是理想变压器.P处有一个与灯泡L2串联的干簧管,原来P处没有磁场.现在让条形磁铁的一端靠近P处,则以下说法正确的是( )| A. | 干簧管与日光灯电路中的启动器工作原理完全相同,在电路中发挥的作用也相同 | |
| B. | 电压表V1的示数不变,电流表A1的示数变大 | |
| C. | 电压表V2的示数增加、电流表A2的示数增加 | |
| D. | 若电压表V3的示数是5伏,则铁芯中磁通量变化率的最大值是5$\sqrt{2}$wb/s |
13. 如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
 如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )
如图所示,物体A分别与水平面、竖直墙面以及物体B紧密接触,所有接触面均光滑,A,B均静止,则( )| A. | 物体A受三个弹力作用 | B. | 物体A受两个弹力作用 | ||
| C. | 物体B受两个弹力作用 | D. | 物体A和物体B均只受一个弹力作用 |
20. 如图所示,皮带运输机正在货物从低处匀速运往高处,运送过程中货物与传送带保持相时静止,则下列说法正确的是( )
如图所示,皮带运输机正在货物从低处匀速运往高处,运送过程中货物与传送带保持相时静止,则下列说法正确的是( )
 如图所示,皮带运输机正在货物从低处匀速运往高处,运送过程中货物与传送带保持相时静止,则下列说法正确的是( )
如图所示,皮带运输机正在货物从低处匀速运往高处,运送过程中货物与传送带保持相时静止,则下列说法正确的是( )| A. | 货物具有相对传送带向上的运动趋势 | |
| B. | 货物具有相对传送带向下的运动趋势 | |
| C. | 货物受传送带的摩擦力沿传送带向上 | |
| D. | 传送带没有给货物摩擦力作用 |
17. 如图,冰壶是冬奥会的正式比赛项目,冰壶在冰面运动时受到的阻力很小,以下有关冰壶的说法正确的是( )
如图,冰壶是冬奥会的正式比赛项目,冰壶在冰面运动时受到的阻力很小,以下有关冰壶的说法正确的是( )
 如图,冰壶是冬奥会的正式比赛项目,冰壶在冰面运动时受到的阻力很小,以下有关冰壶的说法正确的是( )
如图,冰壶是冬奥会的正式比赛项目,冰壶在冰面运动时受到的阻力很小,以下有关冰壶的说法正确的是( )| A. | 冰壶在冰面上的运动直接验证了牛顿第一定律 | |
| B. | 冰壶在冰面上做运动状态不变的运动 | |
| C. | 冰壶在冰面上的运动说明冰壶在运动过程中惯性慢慢减小 | |
| D. | 冰壶在运动过程中抵抗运动状态变化的“本领”是不变的 |
18.下列关于重心、弹力和摩擦力的说法,正确的是( )
| A. | 形状规则的物体的重心一定在物体的几何中心上 | |
| B. | 劲度系数越大的弹簧,产生的弹力越大 | |
| C. | 静摩擦力的大小是在零和最大静摩擦力之间发生变化 | |
| D. | 动摩擦因数与物体之间的压力成反比,与滑动摩擦力成正比 |

