题目内容
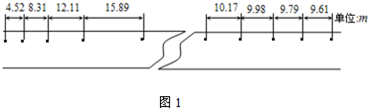
某同学为估测摩托车在水泥路面上行驶时所受的牵引力，设计了下述实验：将输液用的500ml玻璃瓶装适量水后，连同输液管一起绑在摩托车上，调节输液管的滴水速度，刚好每隔1.0s滴一滴，该同学骑摩托车，先使之加速到某一速度，然后熄火，让摩托车沿直线滑行，如图是某次实验中水泥路面上的部分水滴（左侧是起点）．设该同学质量为50kg，摩托车的质量为75kg，根据该同学的实验结果可估算（g=10m/s2） （图中长度单位：m）
（1）骑摩托车行驶至D点时的速度大小为
（2）骑摩托车加速时的加速度大小为
（3）骑摩托车加速时的牵引力大小为
（1）骑摩托车行驶至D点时的速度大小为
14.0
14.0
m/s2（2）骑摩托车加速时的加速度大小为
3.79
3.79
m/s2；（3）骑摩托车加速时的牵引力大小为
497.5
497.5
N．分析：根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上D点时小车的瞬时速度大小．
解答：解：（1）根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，
得：vD=
=
m/s=14.0m/s
（2）已知前四段位移，根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，
得：x4-x2=2a1T2
x3-x1=2a2T2
为了更加准确的求解加速度，我们对两个加速度取平均值
得：a=
（a1+a2）
即小车运动的加速度计算表达式为：
a=
=
=3.79m/s2，
根据第二段纸带解出摩托车减速过程的加速度为：a2=
=0.19m/s2，
由牛顿第二定律：
加速过程：F-f=ma
减速过程：f=ma2，
解得：F=m（a+a2）=（50+75）×（3.79+0.19）N=497.5N
故答案为：14.0，3.79，497.5
得：vD=
| xCE |
| 2T |
| 12.11+15.89 |
| 2×1 |
（2）已知前四段位移，根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，
得：x4-x2=2a1T2
x3-x1=2a2T2
为了更加准确的求解加速度，我们对两个加速度取平均值
得：a=
| 1 |
| 2 |
即小车运动的加速度计算表达式为：
a=
| x4+x3-x2-x1 |
| 4T2 |
| xCE-xAC |
| 4T2 |
根据第二段纸带解出摩托车减速过程的加速度为：a2=
| xFG -xGJ |
| 4T2 |
由牛顿第二定律：
加速过程：F-f=ma
减速过程：f=ma2，
解得：F=m（a+a2）=（50+75）×（3.79+0.19）N=497.5N
故答案为：14.0，3.79，497.5
点评：要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．
练习册系列答案
相关题目
某同学为估测摩托车在水泥路上行驶时的加速度，设计了下述实验：将输液用过的500mL的玻璃瓶装适量水，连同输液管一起绑在摩托车上，调节输液管的滴水速度，使其刚好每隔1.00s滴一滴．该同学骑摩托车，先使之加速至某一速度，然后熄火，让摩托车沿直线滑行．图为某次实验中水泥路面上的部分水滴（左侧为起点）．设该同学质量为50kg，摩托车质量为75kg，g=10m/s2，根据该同学的实验结果可估算：