Question

【题目】如图所示，竖直平面内固定着一个滑槽轨道，其左半部分是倾角为θ=37°，长为l=1m的斜槽PQ，右部是光滑半圆槽QSR，RQ是其竖直直径，两部分滑槽在Q处平滑连接，R、P两点等高，质量为m=0.2kg的小滑块（可看作质点）与斜槽间的动摩擦因数为μ=0.375，将小滑块从斜槽轨道的最高点P释放，使其开始沿斜槽下滑，滑块通过Q点时没有机械能损失，求：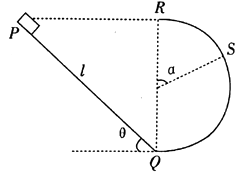

（1）小滑块从P到Q克服摩擦力做的功Wf；
（2）为了使小滑块滑上光滑半圆槽后恰好能到达最高点R，从P点释放时小滑块沿斜面向下的初速度v0的大小．

Answer 1

【答案】
（1）解：小滑块在PQ上受到的摩擦力为：f=μmgcosθ=0.6N

那么，小滑块从P到Q克服摩擦力做的功为：W=fl=0.6J；

答：小滑块从P到Q克服摩擦力做的功Wf为0.6J；

（2）解：由几何关系可得半圆轨道的半径为： ；

小滑块滑上光滑半圆槽后恰好能到达最高点R，那么在R点对小滑块应用牛顿第二定律可得： ；

滑块从P到R的运动过程中，只有摩擦力做功，故由动能定理可得：

解得： ；

答：为了使小滑块滑上光滑半圆槽后恰好能到达最高点R，从P点释放时小滑块沿斜面向下的初速度v0的大小为3m/s

【解析】（1）先求得摩擦力大小，然后按功的定义式求解；（2）根据牛顿第二定律求得在R点的速度，然后对P到R运动过程应用动能定理即可求解．