题目内容
【题目】如图所示,是探究某根弹簧的伸长量x与所受拉力F之间的关系图:
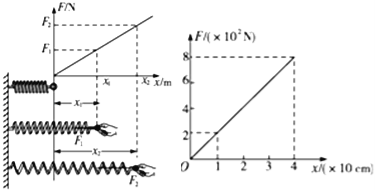
(1)写出图线代表的函数 (x用m作单位);
(2)弹簧的劲度系数是 N/m;
(3)当弹簧受F2=800N的拉力作用时,弹簧伸长量为x2= cm.
【答案】(1)F=2000x,(2)2000;(3)40
【解析】
试题由图象可以看出根弹簧的伸长量X与所受拉力F是线性关系,解出斜率即能找到图线对应的函数,根据胡克定律可以解出弹簧的劲度系数,以及已知拉力时弹簧的形变量.
解:(1)由图象可以解出倾斜直线的斜率,k=![]() =
=![]() =2000N/m
=2000N/m
由于F=kx
解得:F=2000x
(2)根据胡克定律弹簧的弹力与弹簧的形变量成正比,比例系数即为弹簧的劲度系数;所以弹簧的劲度系数为2000N/m.
(3)由胡克定律:F=2000x,当弹簧受F=800N的拉力作用时(在弹性限度内),
弹簧伸长:x=0.4m=40cm
故答案为:(1)F=2000x,(2)2000;(3)40

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目