题目内容
16.在“探究弹力和弹簧伸长的关系”实验中,在弹性限度内,一根弹簧悬挂10N重物时长度为0.50m;悬挂20N重物时,长度为0.60m,则弹簧受到的弹力大小为25N时,弹簧的长度可能为( )| A. | 0.15 m | B. | 0.35 m | C. | 0.55 m | D. | 0.65 m |
分析 弹簧的弹力与形变量遵循胡克定律F=kx,根据胡克定律列出方程组进行求解.
解答 解:设弹簧的原长为l0,根据胡克定律有:F1=k(l1-l0),F2=k(l2-l0),
代入数据有:12=k(0.16-l0),20=k(0.20-l0),
得:l0=0.40m;k=200N/m.
弹簧受到的弹力大小为25N时:25=k(l-l0),
代入数据得:x=0.65m
故D正确,ABC错误.
故选:D
点评 解决本题的关键掌握胡克定律F=kx.该题也可以通过该公式求解:k=$\frac{F}{x}=\frac{△F}{△x}$进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图1所示,并在其上取了A、B、C、D、E、F、G 7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、50Hz交流电源.
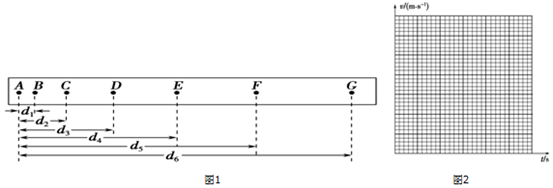
(1)设电火花计时器的周期为T,计算F点的瞬时速度vF的公式为vF=$\frac{{{d_6}-{d_4}}}{10T}$;
(2)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.以A点对应的时刻为t=0,试在图2所示坐标系中合理地选择标度,作出v-t图象,并利用该图象求出物体的加速度a=0.40 m/s2;

(1)设电火花计时器的周期为T,计算F点的瞬时速度vF的公式为vF=$\frac{{{d_6}-{d_4}}}{10T}$;
(2)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.以A点对应的时刻为t=0,试在图2所示坐标系中合理地选择标度,作出v-t图象,并利用该图象求出物体的加速度a=0.40 m/s2;
| 对应点 | B | C | D | E | F |
| 速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
7. 如图,当滑线变阻器的滑动片P向左滑动时,电流表A1的读数变化为△I1,电流表A2的读数变化为△I2,下列说法中正确的是( )
如图,当滑线变阻器的滑动片P向左滑动时,电流表A1的读数变化为△I1,电流表A2的读数变化为△I2,下列说法中正确的是( )
 如图,当滑线变阻器的滑动片P向左滑动时,电流表A1的读数变化为△I1,电流表A2的读数变化为△I2,下列说法中正确的是( )
如图,当滑线变阻器的滑动片P向左滑动时,电流表A1的读数变化为△I1,电流表A2的读数变化为△I2,下列说法中正确的是( )| A. | 电流表A1读数变大,电流表A2读数变小 | |
| B. | 电流表A1读数变大,电流表A2读数变大 | |
| C. | △I1>△I2 | |
| D. | △I1<△I2 |
4.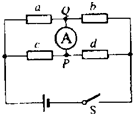 有a、b、c、d四只电阻,其中三只电阻的阻值一样,只有一只电阻的阻值偏大.要找出这只电阻,某同学设计了如图所示的电路.当开关闭合时测出有电流从P流向Q,下列说法正确的是( )
有a、b、c、d四只电阻,其中三只电阻的阻值一样,只有一只电阻的阻值偏大.要找出这只电阻,某同学设计了如图所示的电路.当开关闭合时测出有电流从P流向Q,下列说法正确的是( )
 有a、b、c、d四只电阻,其中三只电阻的阻值一样,只有一只电阻的阻值偏大.要找出这只电阻,某同学设计了如图所示的电路.当开关闭合时测出有电流从P流向Q,下列说法正确的是( )
有a、b、c、d四只电阻,其中三只电阻的阻值一样,只有一只电阻的阻值偏大.要找出这只电阻,某同学设计了如图所示的电路.当开关闭合时测出有电流从P流向Q,下列说法正确的是( )| A. | 阻值偏大的电阻一定是a和d中的一个 | |
| B. | 阻值偏大的电阻一定是c和b中的一个 | |
| C. | 下一步可将a和d互换位置,根据P、Q间电流的流向来判断 | |
| D. | 下一步可将d和c互换位置,根据P、Q间电流的流向来判断 |
1.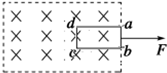 把一个矩形线圈从有理想边界的匀强磁场中匀速拉出,如图所示,第一次速度为v1,第二次速度为v2,且v2=2v1,(已知拉力与线圈所受安培力方向相反)则下列说法正确的是( )
把一个矩形线圈从有理想边界的匀强磁场中匀速拉出,如图所示,第一次速度为v1,第二次速度为v2,且v2=2v1,(已知拉力与线圈所受安培力方向相反)则下列说法正确的是( )
 把一个矩形线圈从有理想边界的匀强磁场中匀速拉出,如图所示,第一次速度为v1,第二次速度为v2,且v2=2v1,(已知拉力与线圈所受安培力方向相反)则下列说法正确的是( )
把一个矩形线圈从有理想边界的匀强磁场中匀速拉出,如图所示,第一次速度为v1,第二次速度为v2,且v2=2v1,(已知拉力与线圈所受安培力方向相反)则下列说法正确的是( )| A. | 两种情况下拉力做的功之比W1:W2=1:2 | |
| B. | 两种情况下拉力的功率之比P1:P2=1:3 | |
| C. | 两种情况下线圈中产生热量之比Q1:Q2=1:4 | |
| D. | 两种情况下通过线圈的电量之比q1:q2=1:1 |
6. 长度均为L的平行金属板AB相距为d,接通电源后,在两板之间形成匀强电场.在A板的中间有一个小孔K,一个带+q的粒子P由A板上方高h处的O点自由下落,从K孔中进入电场并打在B板上K′点处.当P粒子进入电场时,另一个与P相同的粒子Q恰好从两板间距B板$\frac{d}{2}$处的O′点水平飞入,而且恰好与P粒子同时打在K′处.如果粒子进入电场后,所受的重力和粒子间的作用力均可忽略不计,判断以下正确的说法是( )
长度均为L的平行金属板AB相距为d,接通电源后,在两板之间形成匀强电场.在A板的中间有一个小孔K,一个带+q的粒子P由A板上方高h处的O点自由下落,从K孔中进入电场并打在B板上K′点处.当P粒子进入电场时,另一个与P相同的粒子Q恰好从两板间距B板$\frac{d}{2}$处的O′点水平飞入,而且恰好与P粒子同时打在K′处.如果粒子进入电场后,所受的重力和粒子间的作用力均可忽略不计,判断以下正确的说法是( )
 长度均为L的平行金属板AB相距为d,接通电源后,在两板之间形成匀强电场.在A板的中间有一个小孔K,一个带+q的粒子P由A板上方高h处的O点自由下落,从K孔中进入电场并打在B板上K′点处.当P粒子进入电场时,另一个与P相同的粒子Q恰好从两板间距B板$\frac{d}{2}$处的O′点水平飞入,而且恰好与P粒子同时打在K′处.如果粒子进入电场后,所受的重力和粒子间的作用力均可忽略不计,判断以下正确的说法是( )
长度均为L的平行金属板AB相距为d,接通电源后,在两板之间形成匀强电场.在A板的中间有一个小孔K,一个带+q的粒子P由A板上方高h处的O点自由下落,从K孔中进入电场并打在B板上K′点处.当P粒子进入电场时,另一个与P相同的粒子Q恰好从两板间距B板$\frac{d}{2}$处的O′点水平飞入,而且恰好与P粒子同时打在K′处.如果粒子进入电场后,所受的重力和粒子间的作用力均可忽略不计,判断以下正确的说法是( )| A. | P粒子进入电场时速度的平方满足v2=$\frac{d}{4}$a(a为粒子在电场中所受电场力产生的加速度大小) | |
| B. | 将P、Q粒子电量均增为+2q,其它条件不变,P、Q粒子同时进入电场后,仍能同时打在K′点 | |
| C. | 保持P、Q原来的电量不变,将O点和O′点均向上移动相同的距离$\frac{d}{4}$;且使P、Q同时进入电场,则P粒子将先击中K′点 | |
| D. | 其它条件不变,将Q粒子进入电场时的初速度变为原来的2倍,将电源电压也增加为原来的2倍,P、Q同时进入电场,仍能同时打在K′点 |
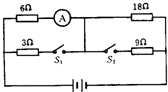 如图所示电路,当S1断、S2闭时,电流表示数为$\frac{3}{5}$A;S1闭、S2断时,电流表示数$\frac{2}{15}$A,求S1、S2均闭合时电流表示数.
如图所示电路,当S1断、S2闭时,电流表示数为$\frac{3}{5}$A;S1闭、S2断时,电流表示数$\frac{2}{15}$A,求S1、S2均闭合时电流表示数.