题目内容
【题目】弹簧原长为l0 , 劲度系数为k。用力把它拉到伸长量为l , 拉力所做的功为W1;继续拉弹簧,使弹簧在弹性限度内再伸长l , 拉力在继续拉伸的过程中所做的功为W2。试求W1与W2的比值。
【答案】因为F=kl , 画出F-l图象,求出图线与横轴所围的面积,其面积就表示弹簧弹力做的功。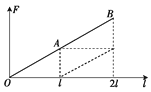
拉力F与弹簧的伸长量l成正比,故在F-l图象中是一条倾斜直线,如图所示,直线与横轴所围的面积表示功的大小。其中,线段OA下的三角形面积表示第一个过程中拉力所做的功W1 , 线段AB下的梯形面积表示第二个过程中拉力所做的功W2。显然,两块面积之比为1∶3,即W1∶W2=1∶3。
【解析】解答:因为F=kl , 画出F-l图象,求出图线与横轴所围的面积,其面积就表示弹簧弹力做的功。 
拉力F与弹簧的伸长量l成正比,故在F-l图象中是一条倾斜直线,如图所示,直线与横轴所围的面积表示功的大小。其中,线段OA下的三角形面积表示第一个过程中拉力所做的功W1 , 线段AB下的梯形面积表示第二个过程中拉力所做的功W2。显然,两块面积之比为1∶3,即W1∶W2=1∶3。
分析:①弹簧弹力是变力,拉伸弹簧时拉力做的功不能用恒力做功的公式计算。
②F-l图象与横轴所围的“面积”等于拉伸弹簧时拉力所做的功,这是计算变力做功时常用的方法。
③从拉力做功的效果出发进行分析:拉力做了功,增加了其他形式的能,这也是计算变力做功常用的方法。
【考点精析】本题主要考查了弹性势能的相关知识点,需要掌握弹性势能是物体由于发生弹性形变而具有的能量才能正确解答此题.

练习册系列答案
相关题目