题目内容
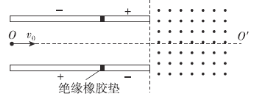
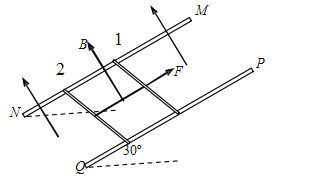
【题目】如图所示,两根足够长的光滑平行金属导轨 MN、PQ间距![]() ,其电阻不计, 两导轨及其构成的平面均与水平面成 30角。杆 1、杆 2 是两根用细线连接的金属杆,分别垂 直导轨放置,每杆两端都与导轨始终接触良好,其质量分别为 m1=0.1kg 和 m2=0.2kg,两杆 的总电阻R=3Ω,两杆在沿导轨向上的外力F作用下保持静止。整个装置处在磁感应强度 B=1T 的匀强磁场中,磁场方向与导轨所在平面垂直,在 t=0 时刻将细线烧断,保持F不变,重力加速度 g=10m/s2,求:
,其电阻不计, 两导轨及其构成的平面均与水平面成 30角。杆 1、杆 2 是两根用细线连接的金属杆,分别垂 直导轨放置,每杆两端都与导轨始终接触良好,其质量分别为 m1=0.1kg 和 m2=0.2kg,两杆 的总电阻R=3Ω,两杆在沿导轨向上的外力F作用下保持静止。整个装置处在磁感应强度 B=1T 的匀强磁场中,磁场方向与导轨所在平面垂直,在 t=0 时刻将细线烧断,保持F不变,重力加速度 g=10m/s2,求:
(1)细线烧断瞬间,杆 1的加速度 a1 的大小;
(2)细线烧断后,两杆最大速度 v1、v2 的大小;
(3)两杆刚达到最大速度时,杆 1 上滑了 0.8 米,则从 t=0 时刻起到此刻用了多长时间?
(4)在(3)题情景中,电路产生的焦耳热。
【答案】(1)10m/s2(2)2m/s ;1m/s(3)0.6s(4)0.9J
【解析】
(1)细线烧断瞬间:
F=(m1+m2)gsin30°
棒1:
F-m1gsin30°=m1a1
解得:
a1=10m/s2
(2)线烧断前:
F=(m1+m2)gsin30°
细线烧断后:
F安1=F安2
方向相反,由系统动量守恒得:
m1v1=m2v2,
两棒同时达到最大速度,之后做匀速直线运动.
对棒2:
m2gsn30°=BI![]() ,
,
I=![]()
解得:
v1=2m/s
v2=1m/s
(3)由系统动量守恒得
m1v1=m2v2
则
m1x1=m2x2
即
x2=04m
设所求时间为t,对棒2由动量定理得:
m2gsin30°·t-B![]() ·t=m2v2-0
·t=m2v2-0
![]()
解得:
t=0.6s
(4)由能量守恒得
Fx1+m2gsin30°·x2=m1gsin30°·x1+![]() +
+![]() +Q
+Q
Q=0.9J

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】某物理兴趣小组对两节电池并联后等效电源的电动势和内阻进行研究如下:将一节电池A和另一节电池 B并联后,接入如图甲所示的测量电路,将虚线框内部看成一个等 效的电源,移动滑动变阻器,测得若干组数据后在图乙中描点。
U/V | 0.89 | 0.78 | 0.67 | 0.56 | 0.58 | 0.34 |
I/A | 0.22 | 0.26 | 0.30 | 0.34 | 0.38 | 0.42 |
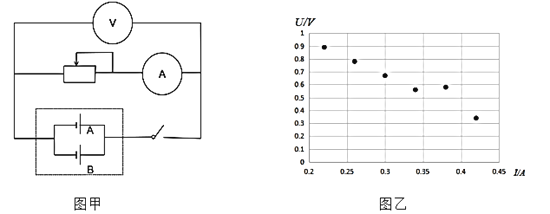
(1)实验过程中小组成员发现当滑动变阻器在阻值较大的范围内调节,电压表的示数变化不明显,其原因是电源内阻____________(填写“较大”或“较小”)
(2)图甲中的电流表和电压表均为非理想电表,下列说法正确的是_____
A.这使得图乙中的U没有测准,U偏大
B.这使得图乙中的U没有测准,U偏小
C.这使得图乙中的 I 没有测准,I偏大
D.这使得图乙中的 I 没有测准,I偏小
(3)根据表中数据在图乙中作出等效电源的![]() 图像,从而得到等效电源的电动势为____________,内阻为____________.(均保留三位有效数字)
图像,从而得到等效电源的电动势为____________,内阻为____________.(均保留三位有效数字)