Question

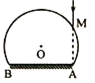
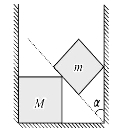
【题目】如图所示，质量为m的正方体和质量为M的正方体放在两竖直墙和水平面间，处于静止状态。m和M的接触面与竖直方向的夹角为，重力加速度为g，若不计一切摩擦，下列说法正确的是

A．水平面对正方体M的弹力大于（M+m）g

B．水平面对正方体M的弹力大小为（M+m）gcos

C．墙面对正方体m的弹力大小为mgtan

D．墙面对正方体M的弹力大小为mgctg

Answer 1

【答案】D

【解析】

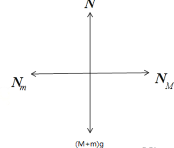
试题分析：对M和m构成的整体进行受力分析，如右侧上图所示，整体受重力（M+m）g、水平面的支持力N，两侧面的支持力Nm和NM，由于两物体受力平衡，根据共点力平衡条件，水平面对正方体M的弹力大小为：N=（M+m）g，故A、B错误．

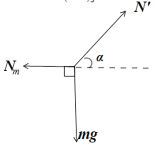
对m进行受力分析，受重力、墙面支持力，M的支持力，如右侧下图所示，在木块受力平衡的过程中，根据共点力平衡条件，有：竖直方向：mg=N′sinα；水平方向：Nm=N′cosα，解得Nm=mgcotα，即墙面对正方体m的弹力大小等于mgcotα．由整体法可知：NM=Nm，则得：墙面对正方体M的弹力大小NM=mgcotα．故C错误，D正确．故选D。