题目内容
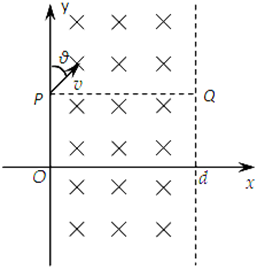
如图,在0≤x≤d的空间,存在垂直xOy平面的匀强磁场,方向垂直xOy平面向里.y轴上P点有一小孔,可以向y轴右侧垂直于磁场方向不断发射速率均为v、与y轴所成夹角θ可在0~1800范围内变化的带负电的粒子.已知θ=45°时,粒子恰好从磁场右边界与P点等高的Q点射出磁场,不计重力及粒子间的相互作用.求:
(1)磁场的磁感应强度;
(2)若θ=30°,粒子射出磁场时与磁场边界的夹角(可用三角函数、根式表示);
(3)能够从磁场右边界射出的粒子在磁场中经过的区域的面积(可用根式表示).
(1)磁场的磁感应强度;
(2)若θ=30°,粒子射出磁场时与磁场边界的夹角(可用三角函数、根式表示);
(3)能够从磁场右边界射出的粒子在磁场中经过的区域的面积(可用根式表示).

(1)当θ=45°时,粒子恰好从磁场右边界与P点等高的Q点射出磁场,
由几何关系可得,d=Rcos45°
解得:R=
d
粒子仅在洛伦兹力作用下,则有:Bqv=m
所以,B=
=
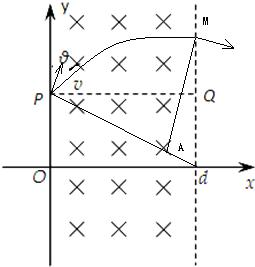
(2)根据半径的大小R=
d与入射角30°,可画出右图,
△AMd中,∠MdA=60°,AM=R,Ad=
-R=
d,
则三角形正弦定理可得,
=
,
设粒子射出磁场时与磁场边界的夹角为β,则有cosβ=sinα=
sin60°=
-
所以θ=arccos(
-
)
(3)根据不同的入射速度方向,画出两种临界状态:一是沿着正y轴方向入射的轨迹;另一是与磁场右边界相切的轨迹
因此能够从磁场右边界射出的粒子在磁场中经过的区域的面积=图上方的扇形面积+下方菱形面积+右边的三角形面积-下方的扇形面积
=下方菱形面积面积+右边的三角形面积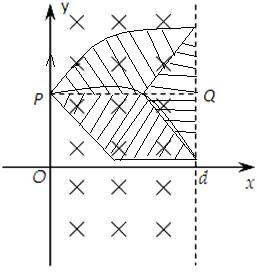 .
.
即有:
d×
d×
+
×(1-
)d×(
d×
+
d)
由几何关系可得,d=Rcos45°
解得:R=
| ||
| 2 |
粒子仅在洛伦兹力作用下,则有:Bqv=m
| v2 |
| R |
所以,B=
| mv |
| Rq |
| ||
| qd |
(2)根据半径的大小R=
| ||
| 2 |
△AMd中,∠MdA=60°,AM=R,Ad=
| d |
| sin60° |
4
| ||||
| 6 |
则三角形正弦定理可得,
| Ad |
| sinα |
| AM |
| sin60° |
设粒子射出磁场时与磁场边界的夹角为β,则有cosβ=sinα=
| Ad |
| AM |
| 2 |
| ||
| 2 |
所以θ=arccos(
| 2 |
| ||
| 2 |
(3)根据不同的入射速度方向,画出两种临界状态:一是沿着正y轴方向入射的轨迹;另一是与磁场右边界相切的轨迹
因此能够从磁场右边界射出的粒子在磁场中经过的区域的面积=图上方的扇形面积+下方菱形面积+右边的三角形面积-下方的扇形面积
=下方菱形面积面积+右边的三角形面积
 .
.即有:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
|


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目