题目内容
一物体从倾角为θ的固定长直斜面顶端由静止开始下滑,已知斜面与物体间的动摩擦因数μ与物体离开斜面顶端距离x之间满足μ=kx(k为已知量),则物体刚下滑时加速度大小为 ,下滑过程中速度最大值为 .(重力加速度为g)
分析:(1)物体刚开始下滑时,位移为0,动摩擦因数为0,此时物体只在重力作用下沿斜面产生加速度;
(2)下滑过程中速度最大时,物体的加速度为0,根据物体平衡求出此时物体的位移,再根据动能定理求出下滑至速度最大时,重力和摩擦力的做功,由动能定理求出最大速度即可.
(2)下滑过程中速度最大时,物体的加速度为0,根据物体平衡求出此时物体的位移,再根据动能定理求出下滑至速度最大时,重力和摩擦力的做功,由动能定理求出最大速度即可.
解答:解:(1)物体刚下滑时,只受重力作用,物体所受重力沿斜面向下的分力F=mgsinθ,根据牛顿第二定律,物体此时产生的加速度
a=
=gsinθ
(2)当物体的加速度为0时,物体的速度最大,故此时物体所受摩擦力与重力沿斜面向下的分力大小相等,即:
f=μmgcosθ=mgsinθ
又因为:μ=kx
所以:kxmgcosθ=mgsinθ可得此时物体的位移x=
从开始下滑到物体速度最大时物体产生的位移为x,故在此过程中重力对物体所做的功为:
WG=mgxsinθ=mg
sinθ
在些过程中摩擦力为变力,摩擦力大小为
f=μmgcosθ=kxmgcoθ摩擦力大小随位移增大而均匀增大,故摩擦力在位移x中的所做的功
Wf=-
mgcosθ?x2=-
kmgcosθ?
根据动能定理有:WG+Wf=
m
-0
∴vmax=
=
故答案为:gsinθ,
a=
| F |
| m |
(2)当物体的加速度为0时,物体的速度最大,故此时物体所受摩擦力与重力沿斜面向下的分力大小相等,即:
f=μmgcosθ=mgsinθ
又因为:μ=kx
所以:kxmgcosθ=mgsinθ可得此时物体的位移x=
| tanθ |
| k |
从开始下滑到物体速度最大时物体产生的位移为x,故在此过程中重力对物体所做的功为:
WG=mgxsinθ=mg
| tanθ |
| k |
在些过程中摩擦力为变力,摩擦力大小为
f=μmgcosθ=kxmgcoθ摩擦力大小随位移增大而均匀增大,故摩擦力在位移x中的所做的功
Wf=-
| 1 |
| 2 |
| 1 |
| 2 |
| tan2θ |
| k |
根据动能定理有:WG+Wf=
| 1 |
| 2 |
| v | 2 max |
∴vmax=
|
|
故答案为:gsinθ,
|
点评:本题关键点一是正确的受力分析知道速度最大时加速度为0,而是求变力做功问题,随位移均匀变化的力做功等于
kx2.
| 1 |
| 2 |

练习册系列答案
相关题目
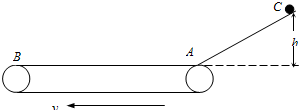 (2009?德阳模拟)如图所示,倾角为300的光滑斜面下端有一水平传送带.一质量为2kg的物体(可视为质点)从离斜面底端高度为3.2m的C 处由静止开始下滑,从A点滑上传送带,传送带固定时,物体刚能滑到AB的中点处.不计在A点的速率变化,物体与传送带间动摩擦因数为μ=0.5,取g=10m/s2
(2009?德阳模拟)如图所示,倾角为300的光滑斜面下端有一水平传送带.一质量为2kg的物体(可视为质点)从离斜面底端高度为3.2m的C 处由静止开始下滑,从A点滑上传送带,传送带固定时,物体刚能滑到AB的中点处.不计在A点的速率变化,物体与传送带间动摩擦因数为μ=0.5,取g=10m/s2



 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上

