题目内容
如图所示,在一个倾角为α足够长的斜面上有一质量为2m的长方形的木板A,木板正好以速度v0沿斜面匀速下滑。当此时将一质量为m的小滑块B轻放在木板表面一端上。若斜面与A和A与B问的动摩擦因数相同,求:
(1)它们间的动摩擦因数为多少?
(2)B在木板A上滑动时,木板A加速度大小为多少?
(3)要使B在木板上滑动不落下,木板A至少为多长?
解:(1)木板A匀速下滑2mgsinα=μ2mgcosα
整理得:μ=tanα
(2)B在木板A上滑动时,B对A的摩擦力
f1=μmgcosα,
斜面对A的摩擦力f2=μ3mgcosα
f1和f2方向均沿斜面向上,根据牛顿第二定律:
f1+f2-2mgsina=2ma
整理得:a=gsina
(3)木板A最小长度是B滑到A另一端时,A、B速度相等,此过程A、B系统动量守恒。
即2mv0=3mv
v=![]() v0
v0
由能量转化守恒定律:A、B摩擦产生热量等A、B系统动能的减少
即Q=AEk
Q=μmgl
△Ek=![]() ×2m
×2m![]() ×3mv2
×3mv2
整理得:l=![]()

练习册系列答案
相关题目
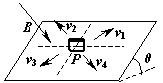 如图所示,在一个倾角为θ的斜面上,有一个带负电的小物体P,空间存在着方向垂直斜面向下的匀强磁场,带电物体与斜面间的摩擦力不能忽略,它在斜面上沿图中所示的哪个方向运动,有可能保持匀速直线的状态不变?
如图所示,在一个倾角为θ的斜面上,有一个带负电的小物体P,空间存在着方向垂直斜面向下的匀强磁场,带电物体与斜面间的摩擦力不能忽略,它在斜面上沿图中所示的哪个方向运动,有可能保持匀速直线的状态不变?
| A.v1方向 | B.v2方向 |
| C.v3方向 | D.v4方向 |
 曾经有科学家采用使物体做匀加速直线运动的方法,来测定物体与斜面间的动摩擦因数,实验装置如图所示,在一个倾角为θ的斜面上,使小木块从静止开始匀加速滑下,实验测得小木块在时间t内的位移为x,已知重力加速度为g.试求:
曾经有科学家采用使物体做匀加速直线运动的方法,来测定物体与斜面间的动摩擦因数,实验装置如图所示,在一个倾角为θ的斜面上,使小木块从静止开始匀加速滑下,实验测得小木块在时间t内的位移为x,已知重力加速度为g.试求: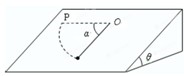 如图所示,在一个倾角为θ=37°(cos37°=0.8)的斜面上,O点固定一根细绳,细绳另一端连接一个质点.现将质点放到斜面上P点,由静止释放,已知OP连线水平且间距为绳长,质点滑动到细绳转过角度α=90°的位置时刚好停止.问:
如图所示,在一个倾角为θ=37°(cos37°=0.8)的斜面上,O点固定一根细绳,细绳另一端连接一个质点.现将质点放到斜面上P点,由静止释放,已知OP连线水平且间距为绳长,质点滑动到细绳转过角度α=90°的位置时刚好停止.问: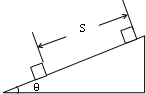 18世纪的瑞士著名科学家欧拉(L.Euler)首先采用使物体做加速运动的方法测定物体的动摩擦因数,实验装置如图所示.在一个倾角为θ的斜面上,使一小木块从静止开始加速下滑.测出时间t内小木块的位移s,即可用t、s和θ得出动摩擦因数的表达式.请推导这个表达式.
18世纪的瑞士著名科学家欧拉(L.Euler)首先采用使物体做加速运动的方法测定物体的动摩擦因数,实验装置如图所示.在一个倾角为θ的斜面上,使一小木块从静止开始加速下滑.测出时间t内小木块的位移s,即可用t、s和θ得出动摩擦因数的表达式.请推导这个表达式.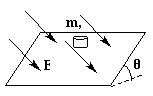 如图所示,在一个倾角为θ的斜面上,有一个质量为m、电量为q的带电物体,空间存在着方向垂直斜面向下的匀强磁场,磁感强度大小为B,带电物体与斜面间的动摩擦因数为μ,它在斜面上沿什么方向、以多大的速度运动,可以保持匀速直线的状态不变?
如图所示,在一个倾角为θ的斜面上,有一个质量为m、电量为q的带电物体,空间存在着方向垂直斜面向下的匀强磁场,磁感强度大小为B,带电物体与斜面间的动摩擦因数为μ,它在斜面上沿什么方向、以多大的速度运动,可以保持匀速直线的状态不变?