题目内容
18. 如图所示,两根长度不同的轻质细绳,一端固定于O点,另一端各系一个完全相同的可以看成质点的小铁球,分别给给两小球一水平速度,两球恰好在同一水平面内做匀速圆周运动,已知∠AOC=60°,∠BOC=30°,则两绳中张力之比FA:FB=$\sqrt{3}$:1;两球运动的周期之比TA:TB=1:1.
如图所示,两根长度不同的轻质细绳,一端固定于O点,另一端各系一个完全相同的可以看成质点的小铁球,分别给给两小球一水平速度,两球恰好在同一水平面内做匀速圆周运动,已知∠AOC=60°,∠BOC=30°,则两绳中张力之比FA:FB=$\sqrt{3}$:1;两球运动的周期之比TA:TB=1:1.
分析 小球靠重力和拉力的合力提供向心力,根据平行四边形定则求出张力大小之比,根据合力提供向心力得出周期的表达式,从而得出周期之比.
解答 解:根据平行四边形定则知,拉力的大小F=$\frac{mg}{cosθ}$,因为∠AOC=60°,∠BOC=30°,则FA:FB=$\sqrt{3}$:1,
由牛顿第二定律得
mgtanθ=mhtanθ$\frac{4{π}^{2}}{{T}^{2}}$,
解得T=$2π\sqrt{\frac{h}{g}}$,则TA:TB=1:1.
故答案为:$\sqrt{3}:1$,1:1.
点评 本题是圆锥摆问题,分析受力,确定向心力是关键.对于圆锥摆的周期与单摆的周期类似,可类比记忆.

练习册系列答案
相关题目
8. 如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
 如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )
如图所示,直线B为电源的U-I图线,直线A为电阻R的U-I图线,该电源和该电阻组成闭合电路时,电源输出功率和电源的效率分别是( )| A. | 电源的输出功率为4W | B. | 电源的输出功率为2W | ||
| C. | 电源效率为33.3% | D. | 电源效率为66.7% |
9.酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间.表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车制动时的加速度大小都相同).
分析表,求解下列问题
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
| 速度(m/s) | 思考距离/m | 制动距离/m | ||
| 正常 | 酒后 | 正常 | 酒后 | |
| 15 | 7.5 | 15.0 | 22.5 | 30.0 |
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
13.某物体沿一直线运动,其v-t图象如图,则下列说法正确的是( )
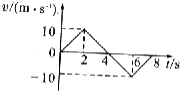

| A. | 第2s内和第3s内速度方向相反 | |
| B. | 第2-4s内和第4-6s内的加速度方向相反 | |
| C. | 第3s内速度方向与加速度方向相反 | |
| D. | 第5s内速度方向与加速度方向相反 |
3.两个完全相同的金属小球,带电量之比为1:5,两带电小球可视为点电荷,在真空中相距为r时,相互作用力为F;若把它们接触后再放回原处,则它们之间的相互作用力可能为( )
| A. | $\frac{9}{5}F$ | B. | $\frac{5}{9}F$ | C. | $\frac{3}{5}F$ | D. | $\frac{4}{5}F$ |
10.一个小铁球和一根羽毛同时从同一高处下落总是铁球先落地,这是因为( )
| A. | 铁球比羽毛重 | B. | 铁球比羽毛密度大 | ||
| C. | 羽毛受到的空气阻力相对大 | D. | 羽毛重力加速度小 |
7.图为根据某次实验记录数据画出的U-I图象,关于这个图象,下列说法正确的是( )
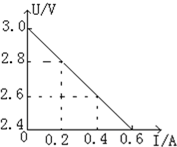

| A. | 由曲线与纵轴的交点可知,电源的电动势E=3V | |
| B. | 横轴截距表示短路电流,即I短=0.6A | |
| C. | 根据r=$\frac{E}{{I}_{短}}$,计算出待测电源的内阻为5Ω | |
| D. | 根据r=$\frac{△U}{△I}$,计算出待测电源的内阻为1Ω |
8.关于点电荷的说法,正确的是( )
| A. | 只有体积很小的带电体,才能作为点电荷 | |
| B. | 点电荷一定是电量很小的电荷 | |
| C. | 当带电体本身的大小和电荷的分布对带电体之间的静电作用力没有影响或几乎没有影响时,就可以将他们看成点电荷 | |
| D. | 体积较大的电荷一定不能当作点电荷 |
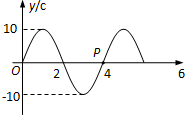 如图为一列沿x轴正方向传播的简谐波在t=0时刻的波形图,已知波速为10m/s,则图中P质点的振动方程为y=10sin5πt(cm)×(判断对错)
如图为一列沿x轴正方向传播的简谐波在t=0时刻的波形图,已知波速为10m/s,则图中P质点的振动方程为y=10sin5πt(cm)×(判断对错)