题目内容
取一根轻质弹簧,上端固定在铁架台上,下端系一金属小球,如图所示.把小球沿竖直方向拉离平衡位置后释放,小球将在竖直方向做简谐运动(此装置也称竖直弹簧振子).将一个电动传感器接到计算机上,就可以测量弹簧快速变化的力,用这种方法测得弹簧对金属小球拉力的大小随时间变化的曲线如图所示,根据此图提供的信息可知:
(1)摆球的摆动周期T=
(2)t=0.2s时摆球正好经过
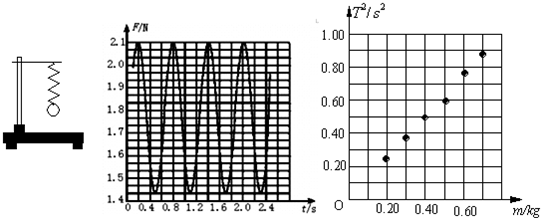
一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系.他多次换用不同质量的小球并测得相应的周期,现将测得的六组数据,用“?”标示在以m为横坐标、T2为纵坐标的坐标纸上,如上图.
(3)根据图中给出的数据作出T2与m的关系图线.
(4)假设图中图线的斜率为b,写出T2与m的关系式为
(5)求得斜率b的值是
(1)摆球的摆动周期T=
0.6
0.6
秒(2)t=0.2s时摆球正好经过
最低点
最低点
.(选填“最低点”、“最高点”或“平衡位置”)
一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系.他多次换用不同质量的小球并测得相应的周期,现将测得的六组数据,用“?”标示在以m为横坐标、T2为纵坐标的坐标纸上,如上图.
(3)根据图中给出的数据作出T2与m的关系图线.
(4)假设图中图线的斜率为b,写出T2与m的关系式为
T2=bm
T2=bm
.(5)求得斜率b的值是
1.25s2/kg.
1.25s2/kg.
.分析:小球通过最低点时弹簧的弹力最大,两次通过最低点的时间间隔等于周期.
根据所描的点作出图线,得出T2与m的关系式.根据图线求出斜率的大小.
根据所描的点作出图线,得出T2与m的关系式.根据图线求出斜率的大小.
解答:解:(1、2)在t=0.2s时,弹簧的弹力最大,知摆球经过最低点,两次经过最低点的时间间隔等于周期,所以T=0.6s.
(3)作出的关系图线如图所示.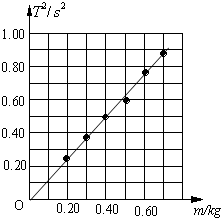
(4)根据图线所知,T2与m成正比,即T2=bm;
(5)图线的斜率b=
≈1.25s2/kg.
故答案为:(1)0.6;(2)最低点.
(3)绘制在右图中.
(4)T2=bm;(5)1.25s2/kg.
(3)作出的关系图线如图所示.

(4)根据图线所知,T2与m成正比,即T2=bm;
(5)图线的斜率b=
| 0.88 |
| 0.70 |
故答案为:(1)0.6;(2)最低点.
(3)绘制在右图中.
(4)T2=bm;(5)1.25s2/kg.
点评:作图连线时,对于偏离直线较远的点可以认为是错误造成的,要舍弃

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 (2008?虹口区二模)取一根轻质弹簧,上端固定在铁架台上,下端系一金属小球,如图甲所示.把小球沿竖直方向拉离平衡位置后释放,小球将在竖直方向做简谐运动(此装置也称竖直弹簧振子).一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系.他多次换用不同质量的小球并测得相应的周期,现将测得的六组数据,用“?”标示在以m为横坐标、T2为纵坐标的坐标纸上,如图乙所示.
(2008?虹口区二模)取一根轻质弹簧,上端固定在铁架台上,下端系一金属小球,如图甲所示.把小球沿竖直方向拉离平衡位置后释放,小球将在竖直方向做简谐运动(此装置也称竖直弹簧振子).一位同学用此装置研究竖直弹簧振子的周期T与小球质量m的关系.他多次换用不同质量的小球并测得相应的周期,现将测得的六组数据,用“?”标示在以m为横坐标、T2为纵坐标的坐标纸上,如图乙所示.

