题目内容
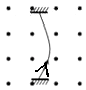
【题目】猴子通过树梢上的藤条越过河流的情景如图所示,图中BC是一条平坦的小路,长为4m,B端离河岸A处的水平距离为3m,AB两点恰好都在以O为圆心的圆周上.树梢上O点有一最大承受力为86N、长为5m、质量不计的藤条自然下垂,其末端刚好落在小路的左端B处.现有一只质量为5kg的猴子从平坦的小路C处由静止开始匀加速奔跑,到B处获得一定的水平速度并抓住藤条末端荡到河岸A处,不计猴子抓住藤条时的能量损失及空气阻力,重力加速度g=10m/s2 . 求猴子从B处安全荡到A处
(1)重力势能的改变量;
(2)在平坦小路B处的最小速度;
(3)在平坦小路上匀加速奔跑的加速度满足的条件.
【答案】
(1)解:如图所示,过A点作OB的垂线,在直角三角形OAD中
xOD= ![]() =
= ![]() =4m
=4m
△EP=mg(xOB﹣xOD)=50×(5﹣4)=50J
答:重力势能的改变量为50J;

(2)解:猴子从B到A的过程中,减少的动能全部转化为重力势能时,速度最小.
![]() mv12=△EP
mv12=△EP
求得v1=2 ![]() m/s
m/s
答:在平坦小路B处的最小速度为2 ![]() m/s;
m/s;
(3)解:猴子在平坦小路上加速,末速度为v1时,加速度最小.
a1= ![]() =
= ![]() =2.5m/s2
=2.5m/s2
猴子抓住藤条时,藤条刚好没有断开的条件,由牛顿第二定律得
T﹣mg=m ![]()
求得v2=6m/s
猴子在平坦小路上加速末速度为v2时,加速度最大.
a2= ![]() =
= ![]() =4.5m/s2
=4.5m/s2
所以,猴子在平坦小路上加速度:2.5m/s2≤a≤4.5m/s2
答:在平坦小路上匀加速奔跑的加速度满足的条件2.5m/s2≤a≤4.5m/s2.
【解析】根据几何知识求出猴子下落的高度,进而求出重力势能的该变量;
猴子从B到A的过程中,减少的动能全部转化为重力势能时,速度最小,根据能量守恒求最小速度;
【考点精析】本题主要考查了机械能守恒及其条件和机械能综合应用的相关知识点,需要掌握在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变;系统初态的总机械能E 1 等于末态的总机械能E 2 ,即E1 =E2;系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ,即ΔE P减 =ΔE K增;若系统只有A、