题目内容
如图甲所示,MN、PQ为间距L="0" .5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计。导轨平面与水平面间的夹角 ,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s2。求:
,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s2。求:

(1)金属棒与导轨间的动摩擦因数μ;
(2)cd离NQ的距离s;
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量;
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式)。
 ,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s2。求:
,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s2。求:
(1)金属棒与导轨间的动摩擦因数μ;
(2)cd离NQ的距离s;
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量;
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式)。
(1)μ=0.5 (2)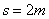 (3)
(3)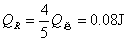 (4)
(4)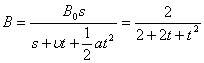
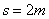 (3)
(3)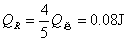 (4)
(4)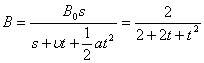
当导体棒速度为零时,只有重力沿斜面向下的分力与滑动摩擦力提供加速度,根据牛顿第二定律求解,求流过横截面的电量时根据平均感应电动势求解,第三问考查电磁感应定律与能量的结合,可根据动能定理求解
(1)当v=0时,a=2m/s2
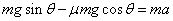
μ=0.5 (3分)
(2)由图像可知:vm=2m/s 当金属棒达到稳定速度时,有
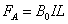
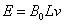
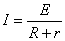
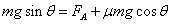
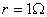
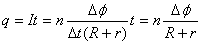
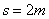 (6分)
(6分)
(3)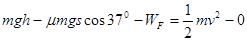
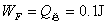
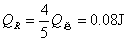 (5分)
(5分)
(4)当回路中的总磁通量不变时,金属棒中不产生感应电流。此时金属棒将沿导轨做匀加速运动。
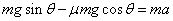
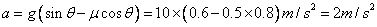
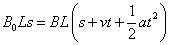
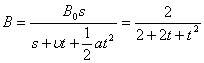 (6分)
(6分)
(1)当v=0时,a=2m/s2
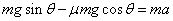
μ=0.5 (3分)
(2)由图像可知:vm=2m/s 当金属棒达到稳定速度时,有
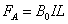
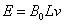
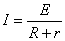
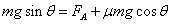
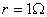
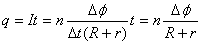
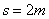 (6分)
(6分)(3)
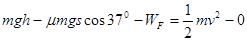
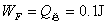
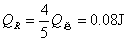 (5分)
(5分) (4)当回路中的总磁通量不变时,金属棒中不产生感应电流。此时金属棒将沿导轨做匀加速运动。
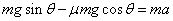
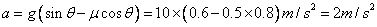
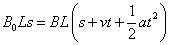
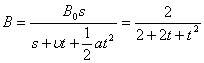 (6分)
(6分) 
练习册系列答案
相关题目



 m的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设进入右侧场时刻t=0, 取g =10m/s2.求:
m的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设进入右侧场时刻t=0, 取g =10m/s2.求: ≈0.19)
≈0.19)


 =30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: