题目内容
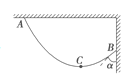
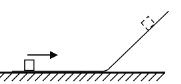
【题目】我国海军歼15舰载机已经在“辽宁”号航母上成功着舰和起飞。现将飞机起飞模型简化为飞机先在水平甲板上做匀加速直线运动,再在倾角为θ=15°的斜面甲板上以最大功率做加速运动,最后从甲板飞出的速度为360 km/h,如图所示。若飞机的质量为18吨,甲板AB长180 m,BC长50 m。(忽略飞机长度,不计一切摩擦和空气阻力,取sin15°=0.3,g=10 m/s2)如果要求到达甲板B点的速度至少为离开斜面甲板速度的60%,则:
(1)飞机在水平甲板上运动时的牵引力至少为多少才能使飞机起飞?
(2)如果到达B点时飞机刚好达到最大功率,则从飞机开始运动到飞离甲板共需多少时间?

【答案】(1)1.8×105 N (2)11.58 s
【解析】
(1)由题意知m=18 t=1.8×104 kg,vC=360 km/h=100 m/s,则B点的速度至少为v=0.6vC=60 m/s,
由动能定理得,
FxAB=![]() mv2,
mv2,
解得:
F=1.8×105 N;
(2)飞机到达B点时的功率:
P=Fv=1.08×107 W,
飞机从A运动到B的时间
t1=![]() ,
,
飞机从B到C的运动过程由动能定理,得
Pt2-mgsinθ·xBC=![]() ,
,
t=t1+t2,
联立解得:
t=11.58 s。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目