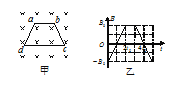题目内容
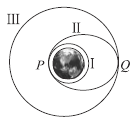
【题目】如图轨道Ⅲ为地球同步卫星轨道，发射同步卫星的过程可以筒化为以下模型：先让卫星进入一个近地圆轨道Ⅰ（离地高度可忽略不计），经过轨道上
点时点火加速，进入椭圆形转移轨道Ⅱ。该椭圆轨道Ⅱ的近地点为圆轨道Ⅰ上的点，远地点为同步圆轨道Ⅲ上的
点。到达远地点时再次点火加速，进入同步轨道Ⅲ。已知引力常量为
，地球质量为
，地球半径为
，飞船质量为
，同步轨道距地面高度为
。当卫星距离地心的距离为
时，地球与卫星组成的系统的引力势能为
（取无穷远处的引力势能为零），忽略地球自转和喷气后飞船质量的変化，问：
（1）在近地轨道Ⅰ上运行时，飞船的动能是多少？
（2）若飞船在转移轨道Ⅱ上运动过程中，只有引力做功，引力势能和动能相互转化。已知飞船在椭圆轨道Ⅱ上运行中，经过点时的速率为
，则经过点时的速率
多大？
（3）若在近地圆轨道Ⅰ上运行时，飞船上的发射装置短暂工作，将小探测器射出，并使它能脱离地球引力范围（即探测器可以到达离地心无穷远处），则探测器离开飞船时的速度
（相对于地心）至少是多少？（探测器离开地球的过程中只有引力做功，动能转化为引力势能）
【答案】（1）
（2）
（3）
【解析】
（1）万有引力提供向心力，求出速度，然后根据动能公式进行求解；
（2）根据能量守恒进行求解即可；
（3）将小探测器射出，并使它能脱离地球引力范围，动能全部用来克服引力做功转化为势能；
（1）在近地轨道（离地高度忽略不计）Ⅰ上运行时，在万有引力作用下做匀速圆周运动
即：
则飞船的动能为
；
（2）飞船在转移轨道上运动过程中，只有引力做功，引力势能和动能相互转化。由能量守恒可知动能的减少量等于势能的増加量：
若飞船在椭圆轨道上运行，经过
点时速率为
，则经过
点时速率为：
；
（3）若近地圆轨道运行时，飞船上的发射装置短暂工作，将小探测器射出，并使它能脱离地球引力范围（即探测器离地心的距离无穷远），动能全部用来克服引力做功转化为势能
即：
则探测器离开飞船时的速度（相对于地心）至少是：
。
