题目内容
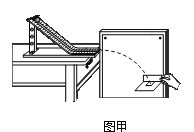
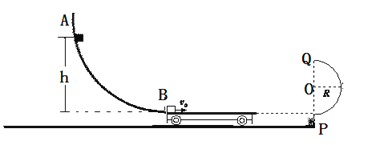
【题目】研究小车运输能力的装置可简化为如图所示的情形,AB为一段光滑弧固定轨道,PQ为光滑半圆弧固定轨道,圆弧半径r=0.2m,水平面光滑.BP长S=3.8m。一长为L=2.8m、质量为M=1kg的平板小车最初停在弧轨道B处,小车上表面略低于B点,且与PQ轨道最低点处于同一水平面。可视为质点、质量为m=4kg的滑块间断从距B点高h=3.2m同一处沿轨道静止滑下,第一块滑块滑上小车后带动小车也向右运动,小车压缩P点下方长度不计的轻弹簧,待滑块离开小车后,小车被弹回原速向左运动,滑块与小车的动摩擦因数为μ=0.8,取g=10m/s2 。
(1)求小车第一次到达P点时的速度大小;
(2)通过计算判断第一块滑块是否滑到Q点;
(3)小车第一次被弹回,当小车左端到达B点时,第二块滑块恰好也运动到B点冲上小车,试判断滑块是否滑离小车,若滑离请求滑块滑出小车时的速度大小。若不滑离,请求小车第二次到P点时的速度大小和第二块滑块滑到Q点时对轨道的压力大小。
【答案】(1)6.4m/s(2)第一块滑块不能滑到Q点(3)260N
【解析】试题分析:根据机械能守恒定律可得滑到低端的速度,根据动量守恒和牛顿第二定律可得小车第一次到达P点时的速度大小;滑块恰能到达Q点,根据牛顿第二定律求出速度,求出第一块滑块在小车上滑行的相对距离,根据能量守恒定律判断第一块滑块是否滑到Q点;根据动量守恒定律求出共同的速度,在由能量守恒定律求出距离,判断出能否滑出小车,第二块滑块滑到Q点,由向心力公式,求出得第二块滑块滑到Q点时对轨道的压力大小。
(1)对滑块,根据机械能守恒定律可得: ![]()
代入数据解得: v0=8m/s
对滑块和小车,由动量守恒定律,得mv0=(m+M)v1
解得:v1=6.4m/s
对滑块,由牛顿第二定律,得 μmg=ma1
解得: a1=8m/s2
由运动学公式可得: ![]()
解得:x1=1.44m
对小车,由牛顿第二定律,得mg=Ma2
解得:a2=32m/s2
由运动学公式,得![]()
解得:x2=0.64m<S-L
小车和滑块共速后到达P点。小车第一次到达P点时的速度大小为 v1=6.4m/s
(2)滑块恰能到达Q点,根据牛顿第二定律: ![]()
解得:vQ=![]()
第一块滑块在小车上滑行的相对距离为:x1=x1-x2=0.8m
由能量守恒定律得: ![]()
解得: ![]() ,故第一块滑块不能滑到Q点。
,故第一块滑块不能滑到Q点。
(3)小车第一次被弹回B点时,对第二块滑块和小车,
由动量守恒定律,得mv0-Mv1=(m+M)v2
解得:v2 =5.12m/s
由能量守恒定律,得![]()
解得:L1=2.6m<L
故第二块滑块不会滑离小车。
分析易知第二块滑块和小车共速时,小车末到达P点,
故小车第二次到P点时的速度大小为v2 =5.12m/s .
第二块滑块在小车上滑行的相对距离: ![]()
由能量守恒定律,得![]()
解得:vQ2![]()
![]()
第二块滑块滑到Q点,由向心力公式,得FN+mg=![]()
解得:FN=260N
由牛顿第三定律,得第二块滑块滑到Q点时对轨道的压力大小![]() FN=260N
FN=260N