题目内容
10.两个共点力的大小分别为F1=6N,F2=3N,设它们的合作力为F,则F和F1之间的夹角最大为30°,此时合力F的大小为$3\sqrt{3}$N.分析 作出F1,以F1的末端为圆心,F2的大小为半径,作圆,根据矢量三角形求出F和F1之间的最大夹角,结合平行四边形定则求出合力F的大小.
解答 解: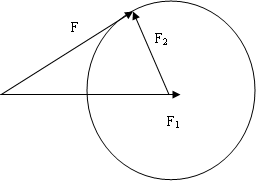 作出F1,以F1的末端为圆心,F2的大小为半径,作圆,如图所示,可知当合力F与F2垂直时,F和F1之间的夹角最大.
作出F1,以F1的末端为圆心,F2的大小为半径,作圆,如图所示,可知当合力F与F2垂直时,F和F1之间的夹角最大.
sinα=$\frac{{F}_{2}}{{F}_{1}}=\frac{3}{6}=\frac{1}{2}$,解得最大夹角α=30°.此时合力的大小F=${F}_{1}cos30°=6×\frac{\sqrt{3}}{2}N=3\sqrt{3}N$.
故答案为:30°,$3\sqrt{3}$
点评 本题考查了力和合成,知道合力与分力遵循平行四边形定则,本题运用三角形定则分析求解比较简捷,知道平行四边形定则和三角形定则的实质是相同的.

练习册系列答案
相关题目
18.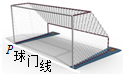 如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
 如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )| A. | 足球位移的大小x=$\sqrt{\frac{{L}^{2}}{4}+{s}^{2}}$ | |
| B. | 足球初速度的大小v0=$\sqrt{\frac{g}{2h}(\frac{{L}^{2}}{4}+{s}^{2})}$ | |
| C. | 足球末速度的大小v=$\sqrt{\frac{g}{2h}(\frac{{L}^{2}}{4}+{s}^{2})+4gh}$ | |
| D. | 足球初速度的方向与球门线夹角的正切值tanθ=$\frac{L}{2s}$ |
5.杂技演员在表演飞车走壁时,在r=4m的竖直筒体内表面某一个高度处做匀速圆周运动.则至少需要的速度为(设轮胎与筒内表面的动摩擦因数为μ=0.4,g取10m/s2)( )
| A. | 10m/s | B. | 5m/s | C. | 7m/s | D. | 15m/s |
15.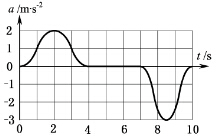 一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
 一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )| A. | t=2s时最大 | B. | t=2s时最小 | C. | t=8.5s时最大 | D. | t=8.5s时最小 |
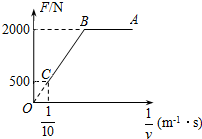 2013年5月18日第九届中国(北京)国际园林博览会开幕,为了方便游客游览,园中引进了无尾气无噪音的电动观光车,某辆电动观光车从静止开始沿平直公路行驶,达到的最大速度为36km/h,在此过程中,电动观光车发动机的牵引力F与对应速度的倒数$\frac{1}{v}$的关系图象如图所示(图中AB、BO均为直线),已知电动观光车的质量为1.2×103kg,行驶中所受的阻力恒定,则该车发动机的额定功率为5000W,从静止开始到发动机的功率达到额定功率所需要的时间为2s.
2013年5月18日第九届中国(北京)国际园林博览会开幕,为了方便游客游览,园中引进了无尾气无噪音的电动观光车,某辆电动观光车从静止开始沿平直公路行驶,达到的最大速度为36km/h,在此过程中,电动观光车发动机的牵引力F与对应速度的倒数$\frac{1}{v}$的关系图象如图所示(图中AB、BO均为直线),已知电动观光车的质量为1.2×103kg,行驶中所受的阻力恒定,则该车发动机的额定功率为5000W,从静止开始到发动机的功率达到额定功率所需要的时间为2s.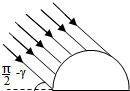 一半径为R的半圆柱形玻璃砖,横截面如图所示.已知玻璃的全反射临界角为γ(γ<$\frac{π}{3}$).与玻璃砖的底平面成($\frac{π}{2}$-γ)角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上.经柱面折射后,有部分光(包括与柱面相切的入射光)能直接从玻璃砖底面射出,若忽略经半圆柱内表面反射后射出的光,求底面透光部分的宽度.
一半径为R的半圆柱形玻璃砖,横截面如图所示.已知玻璃的全反射临界角为γ(γ<$\frac{π}{3}$).与玻璃砖的底平面成($\frac{π}{2}$-γ)角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上.经柱面折射后,有部分光(包括与柱面相切的入射光)能直接从玻璃砖底面射出,若忽略经半圆柱内表面反射后射出的光,求底面透光部分的宽度.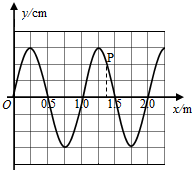 如图为一列沿x轴正方向传播的简谐机械横波某时刻的波形图,质点P的振动周期为0.4s.求该波的波速并判断P点此时的振动方向.
如图为一列沿x轴正方向传播的简谐机械横波某时刻的波形图,质点P的振动周期为0.4s.求该波的波速并判断P点此时的振动方向.