题目内容
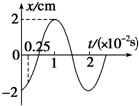 一质点做简谐运动,其位移和时间关系如图所示.
一质点做简谐运动,其位移和时间关系如图所示.(1)求t=0.25×10-2s时的位移;
(2)在t=1.5×10-2s到2×10-2s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?
(3)在t=0到8.5×10-2s时间内,质点通过的位移、路程各多大?
分析:(1)先写出振动方程,再将t=0.25×10-2s代入,求出位移.
(2)由图象直接分析位移如何变化,抓住其他量与位移的关系分析各量的变化情况.
(3)根据时间与周期的关系,结合质点在一个周期内通过的路程是四个振幅,求出路程,并确定出位移.
(2)由图象直接分析位移如何变化,抓住其他量与位移的关系分析各量的变化情况.
(3)根据时间与周期的关系,结合质点在一个周期内通过的路程是四个振幅,求出路程,并确定出位移.
解答:解:(1)由题图可知振幅 A=2cm,周期 T=2×10-2s.
质点的振动方程为:x=Asin(ωt-
)=-Acosωt=-2cos
t cm=-2cos100πt cm
当t=0.25×10-2s时,x=-2cos
cm=-
cm.
(2)由图可知在1.5×10-2 s~2×10-2 s的振动过程中,质点的位移变大,远离平衡位置,则回复力变大,速度变小,动能变小,势能变大.
(3)从t=0至8.5×10-2s时间内为
个周期,质点的路程为s=17A=17×2cm=34cm,位移为2cm.
答:
(1)t=0.25×10-2s时的位移为-
cm;
(2)在t=1.5×10-2s到2×10-2s的振动过程中,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.
(3)在t=0到8.5×10-2s时间内,质点通过的位移为2cm,、路程为34cm.
质点的振动方程为:x=Asin(ωt-
| π |
| 2 |
| 2π |
| 2×10-2 |
当t=0.25×10-2s时,x=-2cos
| π |
| 4 |
| 2 |
(2)由图可知在1.5×10-2 s~2×10-2 s的振动过程中,质点的位移变大,远离平衡位置,则回复力变大,速度变小,动能变小,势能变大.
(3)从t=0至8.5×10-2s时间内为
| 17 |
| 4 |
答:
(1)t=0.25×10-2s时的位移为-
| 2 |
(2)在t=1.5×10-2s到2×10-2s的振动过程中,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.
(3)在t=0到8.5×10-2s时间内,质点通过的位移为2cm,、路程为34cm.
点评:此题关键运用数学知识写出振动方程,知道振动方程的一般表达式:x=Asin(ωt+φ0),即可求得任意时刻的位移,并掌握加速度、回复力等等物理量的关系.

练习册系列答案
相关题目
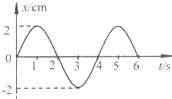 一质点做简谐运动,其对平衡位置的位移x随时间t变化图象如图所示,由此可知( )
一质点做简谐运动,其对平衡位置的位移x随时间t变化图象如图所示,由此可知( )| A、质点振动的振幅是2cm | B、质点振动的频率是4Hz | C、t=2s时质点的速度最大,且方向向下 | D、t=5s时质点所受的合外力为零 |
 一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知,在t=4s时,质点的( )
一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知,在t=4s时,质点的( ) 一质点做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )
一质点做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )