题目内容
 一质点做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )
一质点做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知( )分析:质点的振幅等于振子的位移最大值,由图直接读出振幅和周期,由公式f=
求出频率.根据给定时刻以后质点位移的变化,分析速度的方向,由简谐运动的特征a=-
分析加速度的大小.根据牛顿第二定律回复力的大小与加速度大小成正比.
| 1 |
| T |
| kx |
| m |
解答:解:A、由图读出周期T=4s,则频率f=
=0.25Hz,故A错误;
B、t=2s时,质点的位移最大,则由a=-
知加速度最大,故B错误;
C、由图读出振幅为2cm,C正确;
D、t=3s时,质点位于平衡位置,位移x=0,则由a=-
知加速度为零,则回复力为零,故D错误;
故选:C.
| 1 |
| T |
B、t=2s时,质点的位移最大,则由a=-
| kx |
| m |
C、由图读出振幅为2cm,C正确;
D、t=3s时,质点位于平衡位置,位移x=0,则由a=-
| kx |
| m |
故选:C.
点评:本题简谐运动的图象能直接读出振幅和周期.对于质点的速度方向,也可以根据斜率读出.简谐运动的特征a=-
,是分析加速度常用的方法.
| kx |
| m |

练习册系列答案
相关题目
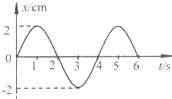 一质点做简谐运动,其对平衡位置的位移x随时间t变化图象如图所示,由此可知( )
一质点做简谐运动,其对平衡位置的位移x随时间t变化图象如图所示,由此可知( )| A、质点振动的振幅是2cm | B、质点振动的频率是4Hz | C、t=2s时质点的速度最大,且方向向下 | D、t=5s时质点所受的合外力为零 |
 一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知,在t=4s时,质点的( )
一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知,在t=4s时,质点的( )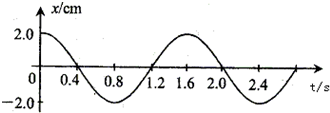
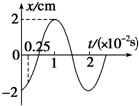 一质点做简谐运动,其位移和时间关系如图所示.
一质点做简谐运动,其位移和时间关系如图所示.