题目内容
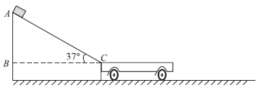
【题目】如图所示,在光滑水平面上,一辆质量M=2kg、长度L = 9. 6m、上表面粗糙的平板车紧 靠着被固定的斜面体ABC,斜面体斜边AC长s = 9m、倾角![]() 。现将质量m=lkg的小木块从斜面顶端A处由静止释放,小木块滑到C点后立即速度大小不变地水平冲上平板车。已 知平板车上表面与C点等高,小木块与斜面、平板车上表面的动摩擦系数分别为
。现将质量m=lkg的小木块从斜面顶端A处由静止释放,小木块滑到C点后立即速度大小不变地水平冲上平板车。已 知平板车上表面与C点等高,小木块与斜面、平板车上表面的动摩擦系数分别为![]() =0.5、
=0.5、![]() = 0.2,sin37°= 0. 6 ,cos37 = 0. 8,g 取 10m/s2,求:
= 0.2,sin37°= 0. 6 ,cos37 = 0. 8,g 取 10m/s2,求:
(1)小木块滑到C点时的速度大小?
(2)试判断小木块能否从平板车右侧滑出,若不能滑出,请求出最终小木块会停在距离车右端多远?若能滑出,请求出小木块在平板车上运动的时间?
【答案】(1)6m/s(2)不会滑出,停在距车右端3.6m
【解析】
(1)木块在斜面上做匀加速直线运动,根据牛顿第二定律可得:mgsin37°-f=ma
其中:f=μ1mgcos37°
解得a=2m/s2,
根据速度位移关系可得v2=2as
解得v=6m/s;
(2)木块滑上车后做匀减速运动,根据牛顿第二定律可得:μ2mg=ma1
解得:a1=2m/s2
车做匀加速直线运动,根据牛顿第二定律可得:μ2mg=Ma2
解得a2=1m/s2,
经过t时间二者的速度相等,则:v-a1t=a2t
解得t=2s
t时间木块的位移x1=vt-![]() a1t2
a1t2
t时间小车的位移x2=![]() a2t2
a2t2
则△x=x1-x2=6m
由于△x=8m<L,所以木块没有滑出,且木块距离车右端距离d=L-△x=3.6m

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目