题目内容
【题目】电动汽车在行驶过程中,消耗电池能量对外做功使汽车前进。汽车安装的电池常用两个物理量衡量其性能,见下表:
物理量 | 定义 | 单位 |
电池容量 | 电池存储电量的多少 | mAh |
电池的能量密度ρ | 单位质量携带电能的多少 | Wh/kg |
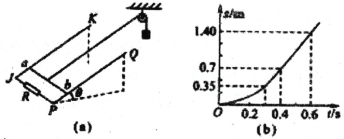
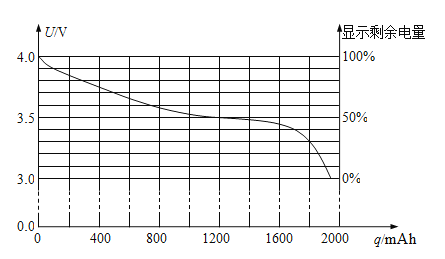
某质量m=0.056kg的电池以恒定电流放电时,端电压与流过电池电量的关系如下图所示。电池容量检测系统在电压为4V时显示剩余电量100%,电压为3V时显示剩余电量0%。通过计算机测得曲线与电量轴所围的面积约为7000V·mAh。
(1)该曲线与电量轴所围面积的物理意义是什么?
(2)该电池的能量密度ρ是多少?
(3)在放电过程中剩余电量从100%到80%用了时间t,由图像推测剩余电量从50%到30%约要多少时间?
(4)某电动汽车除电池外总质量为M,配上质量为m、能量密度为ρ的电池,单次充电后可以在水平路面行驶距离s(s较长,近似认为全程匀速行驶),行驶中所受阻力与总质量成正比,比例系数为k。假设电池能量的![]() 用来对外做功使汽车前进,写出汽车行驶距离s的表达式。为提升电动车单次充电行驶最大距离,国家大力支持研发提高电池的能量密度,而不是仅靠增加车上电池质量,请通过分析说明原因。
用来对外做功使汽车前进,写出汽车行驶距离s的表达式。为提升电动车单次充电行驶最大距离,国家大力支持研发提高电池的能量密度,而不是仅靠增加车上电池质量,请通过分析说明原因。
【答案】(1)表示对外做功的值
(2)125Wh/kg
(3)2t
(4)提高电池的能量密度ρ比增加电池质量m更合理
【解析】
(1)根据图像的坐标轴可知,图像所围面积物理意义是U·It,表示对外做功的值;
(2)由(1)知,能量密度
![]()
(3)q=It,I不变则电量与时间成正比,由U-q图像可知剩余电量从100![]() 到80
到80![]() ,通过电池电量约300mAh,剩余电量从50
,通过电池电量约300mAh,剩余电量从50![]() 到30
到30![]() ,通过电池电量约600mAh,则时间约为2t
,通过电池电量约600mAh,则时间约为2t
(4)设汽车质量M,电池质量m,单次充电行驶最大距离s,由题意,阻力与总质量成正比,即
f=k(m +M)
汽车消耗电能,克服阻力做功
fs=k(m +M)s
电池能量的![]() 用来对外做功
用来对外做功
W=fs =![]() mρ
mρ
单次充电行驶最大距离
![]() <
<![]()
s与m为非线性关系,有上限。可见行驶的最大距离随着电池质量的增加,提升得越来越慢。s与ρ成正比,ρ增大并不增加阻力,不造成电能额外损耗,可见,提高电池的能量密度ρ比增加电池质量m更合理。

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案