题目内容
 如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β,AB及AC两边上分别套用有细线连着的铜环P、Q,当它们静止时,细线跟AB所成的角θ的大小为(细线长度小于BC)( )
如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β,AB及AC两边上分别套用有细线连着的铜环P、Q,当它们静止时,细线跟AB所成的角θ的大小为(细线长度小于BC)( )分析:本题可以运用假设法分析θ与β的关系.假设AC上的环质量为零,则知平衡时θ=β;假设AB上的铜环P的质量为零,平衡时则有θ=
,再分析两环有质量时的角度的关系.
| π |
| 2 |
解答:解:假设AC上的铜环质量为零,重力为零,它仅受线的拉力和铁丝AC的弹力,它们是一对平衡力.由于铁丝对AC上的环的弹力垂直于AC,则细线必定垂直于AC,则细线平行于BC,此时θ=α.但实际上AC上的环的质量大于零,重力大于零,要使此环处于静止,细线的左端必须斜向左上方,则有θ>β.
假设AB上的铜环P的质量为零,重力为零,它仅受细线的拉力和铁丝AB的弹力,它们是一对平衡力,则此环平衡时,细线与AB垂直,θ=
,而AB上的铜环的质量大于零,重力大于零,要使此环处于静止状态,细线不能与AB垂直,应有θ<
,故β<θ<
.
故选D.
假设AB上的铜环P的质量为零,重力为零,它仅受细线的拉力和铁丝AB的弹力,它们是一对平衡力,则此环平衡时,细线与AB垂直,θ=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选D.
点评:本题运用假设法的思维方法,也可以通过分析两环的受力情况,由平衡条件,根据正交分解法确定θ的范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,在AB和AC两边上分别套有用细线连接的铜环,当它们静止时,细线跟AB所成的角度的大小为(细线长度小于BC)( )
如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,在AB和AC两边上分别套有用细线连接的铜环,当它们静止时,细线跟AB所成的角度的大小为(细线长度小于BC)( )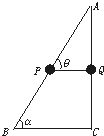 如图所示,用光滑的粗铁丝做成一直角三角形,BC水平,AC边竖直,∠ABC=α,AB及AC两边上分别套有细线连接着的铜环P和铜环Q,当它们静时,细线跟AB所成的角θ的大小为(细线长度小于BC)( )
如图所示,用光滑的粗铁丝做成一直角三角形,BC水平,AC边竖直,∠ABC=α,AB及AC两边上分别套有细线连接着的铜环P和铜环Q,当它们静时,细线跟AB所成的角θ的大小为(细线长度小于BC)( ) 如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β.AB边及AC两边上分别套有用细线相连的铜环(其总长度小于BC边长),当它们静止时,细线跟AB所成的角θ的大小为( )
如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β.AB边及AC两边上分别套有用细线相连的铜环(其总长度小于BC边长),当它们静止时,细线跟AB所成的角θ的大小为( ) 如图所示,用光滑的粗铁丝做成一个直角三角形框架,框架静止放置时BC边水平、AC边竖直,且∠ABC=β,AB及AC两边上分别套有用细线系着的铜环.那么,当它们均静止平衡时,两环之间的细线与框架的AB斜边所成的夹角θ的范围是
如图所示,用光滑的粗铁丝做成一个直角三角形框架,框架静止放置时BC边水平、AC边竖直,且∠ABC=β,AB及AC两边上分别套有用细线系着的铜环.那么,当它们均静止平衡时,两环之间的细线与框架的AB斜边所成的夹角θ的范围是