题目内容
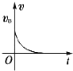
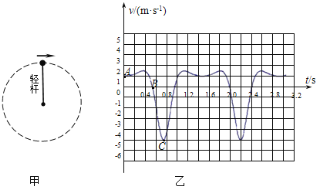
【题目】如图甲所示,轻杆一端与质量为1kg、可视为质点的小球相连,另一端可绕光滑固定轴在竖直平面内自由转动,现使小球在竖直平面内做圆周运动,经最高点开始计时,取水平向右为正方向,小球的水平分速度v随时间t的变化关系如图乙所示,A、B、C三点分别是图线与纵轴、横轴的交点、图线上第一周期内的最低点,该三点的纵坐标分别是1、0、![]() 取
取![]() ,不计空气阻力,下列说法正确的是
,不计空气阻力,下列说法正确的是![]()
![]()
A. 轻杆的长度为![]()
B. 小球经最高点时,杆对它的作用力方向竖直向上
C. B点对应时刻小球的速度为![]()
D. 曲线AB段与坐标轴所围图形的面积为![]()
【答案】B
【解析】
已知小球在ABC三个点的速度,A到C的过程中机械能守恒,由机械能守恒定律即可求出杆的长度;结合小球过最高点的受力的特点,即可求出杆对小球的作用力的方向;由机械能守恒可以求出B点的速度;由于y轴表示的是小球在水平方向的分速度,所以曲线AB段与坐标轴所围图形的面积表示A到B的过程小球在水平方向的位移.
设杆的长度为L,小球从A到C的过程中机械能守恒,得:![]() ,解得
,解得![]() ,故A错误。若小球在A点恰好对杆的作用力是0,则有
,故A错误。若小球在A点恰好对杆的作用力是0,则有![]() ,解得
,解得![]() 。由于小球在A点的速度小于临界速度,所以小球做圆周运动需要的向心力小于重力,杆对小球的作用力的方向向上,故是竖直向上的支持力。故B正确。小球从A到B的过程中机械能守恒,得
。由于小球在A点的速度小于临界速度,所以小球做圆周运动需要的向心力小于重力,杆对小球的作用力的方向向上,故是竖直向上的支持力。故B正确。小球从A到B的过程中机械能守恒,得![]() ,所以
,所以![]() ,故C错误。由于y轴表示的是小球在水平方向的分速度,所以曲线AB段与坐标轴所围图形的面积表示A到B的过程小球在水平方向的位移,大小等于杆的长度,即
,故C错误。由于y轴表示的是小球在水平方向的分速度,所以曲线AB段与坐标轴所围图形的面积表示A到B的过程小球在水平方向的位移,大小等于杆的长度,即![]() 。故D错误。故选B。
。故D错误。故选B。

练习册系列答案
相关题目