题目内容
如右图所示,一质量为m、电荷量为+q的粒子,以速度 从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴进入场强为E、方向与x轴负方向成60°角斜向下的匀强电场中,速度方向与 x轴正方向的夹角为30°,经过一段时间后恰好通过b点正下方的c点,粒子的重力不计.试求:
从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x轴进入场强为E、方向与x轴负方向成60°角斜向下的匀强电场中,速度方向与 x轴正方向的夹角为30°,经过一段时间后恰好通过b点正下方的c点,粒子的重力不计.试求:
(1)圆形匀强磁场的最小面积.
(2)c点到b点的距离d.
(1) (2)
(2)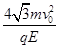
解析试题分析: 很显然,弦长 即为圆形磁场区域的最小直径.
即为圆形磁场区域的最小直径.
(1) 粒子在磁场中做匀速圆周运动,由 得
得
粒子经过磁场区域速度偏转角为120°,这表明在磁场区域中运动轨迹为半径为R的 圆弧,作出粒子运动轨迹如图中实线所示.所求圆形磁场区域的最小半径为
圆弧,作出粒子运动轨迹如图中实线所示.所求圆形磁场区域的最小半径为
r= =Rsin 60°=
=Rsin 60°=
面积为S=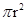 =
= .
.
(2)粒子进入电场做类平抛运动,从b到c垂直电场方向位移为 ①
①
沿电场方向位移为 ②
② =tan 30°③
=tan 30°③
解方程①②③得x′=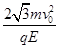


考点:考查了带电粒子在组合场中的运动
点评:带电粒子在匀强磁场和匀强电场中的运动是物理学中的核心知识和重点知识,是学习物理必须掌握的重点基本规律,是高考的重点和热点.解答本题的关键是,按题目中所述的运动方向,根据速度方向和轨道半径垂直的关系,找出粒子做匀速圆周运动的圆心O′.

 名师点拨卷系列答案
名师点拨卷系列答案 如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平 面(纸面)垂直,磁场边界的间距为L。一个质量为m、一边长度也为L的方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直且线框上、下边始终与磁场的边界平行。t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为 。经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置Ⅱ),导线框的速度刚好为零。此后,导线框下落,经过一段时间回到初始位置I(不计空气阻力),则
。经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置Ⅱ),导线框的速度刚好为零。此后,导线框下落,经过一段时间回到初始位置I(不计空气阻力),则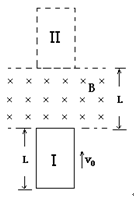
| A.上升过程中,导线框做匀变速运动 |
| B.上升过程克服重力做功的平均功率小于下降过程重力的平均功率 |
| C.上升过程中线框产生的热量比下降过程中线框产生的热量的多 |
| D.上升过程中合力做的功与下降过程中合力做的功相等 |
在倾角为θ足够长的光滑斜面上,存在着两个磁感应强度大小相等的匀强磁场,磁场方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为L,如图所示。一个质量为m、电阻为R、边长也为L的正方形线框在t=0时刻以速度v0进入磁场,恰好做匀速直线运动,若经过时间t0,线框ab边到达gg′与ff′中间位置时,线框又恰好做匀速运动,则下列说法正确的是( )
| A.当ab边刚越过ff′时,线框加速度的大小为gsinθ |
B.t0时刻线框匀速运动的速度为 |
C.t0时间内线框中产生的焦耳热为 |
| D.离开磁场的过程中线框将做匀速直线运动 |

 小球距N点的距离s为多远。
小球距N点的距离s为多远。
 大小、方向如何?
大小、方向如何?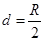 的电子在圆形磁场中运动了多长时间?
的电子在圆形磁场中运动了多长时间?
 延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
 ,小球所受重力不能忽略.求:
,小球所受重力不能忽略.求:
