题目内容
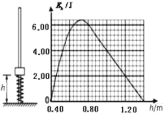
【题目】如图所示,竖直光滑杆固定不动,套在杆上的轻质弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.40 m处,滑块与弹簧不拴接。现由静止释放滑块,通过传感器测量出滑块的速度和离地高度h,计算出滑块的动能EK,并作出滑块的EK—h图象,其中高度从0.80 m上升到1.40m范围内图象为直线,其余部分为曲线。若以地面为重力势能的零势能面,取g=10 m/s2,则结合图象可知( )
A.滑块的质量为1.00 kg
B.弹簧原长为0.72 m
C.弹簧最大弹性势能为10.00 J
D.滑块的重力势能与弹簧的弹性势能总和最小为3.60J
【答案】AC
【解析】
试题分析:在EK—h图象中,图线的斜率表示了滑块所受的合外力,由于高度从0.80m上升到1.40m范围内图象为直线,说明滑块在此范围内离开弹簧,只受重力,所以在h=0.80m处滑块与弹簧分离,即弹簧原长为0.80m,故B错误;在此范围内,图线的斜率绝对值为:![]() ,又
,又![]() ,所以滑块质量
,所以滑块质量![]() ,故A正确;=mg=2N,所以:m=0.2kg,故选项B错误;根据能的转化与守恒可知,当滑块上升至最大高度时,增加的重力势能即为弹簧最大弹性势能,所以
,故A正确;=mg=2N,所以:m=0.2kg,故选项B错误;根据能的转化与守恒可知,当滑块上升至最大高度时,增加的重力势能即为弹簧最大弹性势能,所以![]() ,故C正确;在滑块运动的全过程中,滑块与弹簧组成的系统机械能守恒,即动能、重力势能、弹性势能总量保持不变,因此动能最大时,滑块的重力势能与弹簧的弹性势能总和最小,根据能量守恒定律可知,滑块的重力势能与弹簧的弹性势能总和的最小值Emin等于机械能总量减去滑块的最大动能,即
,故C正确;在滑块运动的全过程中,滑块与弹簧组成的系统机械能守恒,即动能、重力势能、弹性势能总量保持不变,因此动能最大时,滑块的重力势能与弹簧的弹性势能总和最小,根据能量守恒定律可知,滑块的重力势能与弹簧的弹性势能总和的最小值Emin等于机械能总量减去滑块的最大动能,即![]() ,故D错误。
,故D错误。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目