题目内容
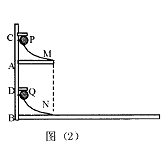
【题目】如图所示，在竖直平面内有光滑轨道ABCD，其中BC是半径为R的四分之一圆弧轨道，AB是竖直轨道，CD是水平轨道。 AB与BC相切于B点，CD与BC相切于C点。一根长为2R的轻杆两端分别固定着两个质量均为m的相同小球P、Q(视为质点)，从Q与B等高处由静止释放，两球滑到水平轨道上。重力加速度为g，则下列说法中正确的是( )
A. 下滑的整个过程中P球机械能守恒
B. 下滑的整个过程中两球与轻杠构成的系统机械能不守恒
C. Q球过C点的速度大小为
D. 下滑的整个过程中Q球机械能增加量为
【答案】D
【解析】A、P球运动过程中轻杆要做功，所以机械能不守恒，故A错误；
B、把两个球和轻杆作为一个系统来研究的话，除了重力和系统内的弹力做功，没有别的力做功，符合机械能守恒的条件，故B错误；
C、Q球过C点时,杆与竖直方向的夹角的余弦: 
,故
;
根据机械能守恒定律,有:
杆不可伸长,故两个球沿着杆方向的分速度相等,故:
联立计算得出:
故C错误;
D、下滑的整个过程中,根据机械能守恒定律,有:
计算得出: 
故Q球机械能增加量为: 
;所以D选项是正确的;
综上所述本题答案是：D
练习册系列答案
相关题目
